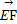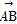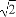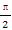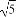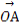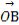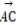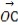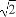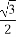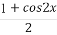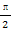Question

已知平面向量a=(x1,y1),b=(x2,y2),若|a|=2,|b|=3,a·b=-6,则=　　　　.

 

Answer 1

-

【解析】【思路点拨】根据条件求出向量的夹角,进而寻求向量坐标间的关系,化简求值即可.

【解析】
设a,b的夹角为θ,则a·b=|a||b|cosθ=-6,

∴cosθ=-1,∴θ=180°.

即a,b共线且反向.

又∵|a|=2,|b|=3,

∴a=-b,x1=-x2,y1=-y2,

∴=-.