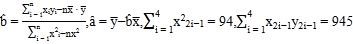题目内容
【题目】函数![]() ,
,![]() .
.
(1)求函数![]() 的单调区间及极值;
的单调区间及极值;
(2)若![]() ,
,![]() 是函数
是函数![]() 的两个不同零点,求证:①
的两个不同零点,求证:①![]() ;②
;②![]() .
.
【答案】(1)在![]() 递减,
递减,![]() 递增,
递增,![]() ,无极大值(2)见解析
,无极大值(2)见解析
【解析】分析:(1)求出![]() ,解不等式
,解不等式![]() 得增区间,解不等式
得增区间,解不等式![]() 得减区间,从而也可得到极值;
得减区间,从而也可得到极值;
(2)①先确定函数的变化趋势,由函数式,知![]() 或
或![]() 时,都有
时,都有![]() ,从而要有两个零点,则必有
,从而要有两个零点,则必有![]() ,从而得
,从而得![]() .因此两个零点
.因此两个零点![]() ,不妨设
,不妨设![]() ,通过构造函数
,通过构造函数![]() ,由
,由![]() 的单调性可证
的单调性可证![]() ,即
,即![]() ,最后由
,最后由![]() 的单调性,得证
的单调性,得证![]() ,②证明:令
,②证明:令![]() ,然后证明
,然后证明![]() =
=![]() ,由
,由![]() ,得
,得![]() ,计算
,计算
![]() ,由
,由![]() 由
由![]() 得
得![]() ,再由
,再由![]() 在
在![]() 上的单调性可证结论.
上的单调性可证结论.
详解:(1)定义域:![]()
![]()
令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]()
∴![]() 在
在![]() 递减,
递减,![]() 递增
递增
∴![]() ,无极大值
,无极大值
(2)由(1)知![]() 时,
时,![]() ;
;![]() 时,
时,![]()
要使![]() 有两个不同零点,则
有两个不同零点,则![]() 即
即![]()
不妨设![]() ,
,
①证明:令![]() ,则
,则![]()
![]() 在
在![]() 递增而
递增而![]() ,∴
,∴![]()
∴![]() 即
即![]()
∵![]() ,∴
,∴![]()
∵![]() 且
且![]() 在
在![]() 递减
递减
∴![]() ,即
,即![]()
②证明:令![]() ,下面先证明
,下面先证明![]() ,
,![]()
∵![]() ,
,![]() ,∴
,∴![]() 在
在![]() 递增
递增
∴![]() ,∴
,∴![]() 在
在![]() 递增,∴
递增,∴![]()
即![]() 在
在![]() 总成立,∵
总成立,∵![]() ,∴
,∴![]()
又![]()
∵![]() 由
由![]() 知
知![]() ,
,![]()
又![]() ,
,![]() 且
且![]() 及
及![]() 在
在![]() 递减
递减
∴![]() ,即
,即![]()

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
【题目】某企业2018年招聘员工,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五种岗位的应聘人数、录用人数和录用比例(精确到1%)如下:
五种岗位的应聘人数、录用人数和录用比例(精确到1%)如下:
岗位 | 男性 应聘人数 | 男性 录用人数 | 男性 录用比例 | 女性 应聘人数 | 女性 录用人数 | 女性 录用比例 |
| 269 | 167 |
| 40 | 24 |
|
| 40 | 12 |
| 202 | 62 |
|
| 177 | 57 |
| 184 | 59 |
|
| 44 | 26 |
| 38 | 22 |
|
| 3 | 2 |
| 3 | 2 |
|
总计 | 533 | 264 |
| 467 | 169 |
|
(1)从表中所有应聘人员中随机选择1人,试估计此人被录用的概率;
(2)从应聘![]() 岗位的6人中随机选择2人.记
岗位的6人中随机选择2人.记![]() 为这2人中被录用的人数,求
为这2人中被录用的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)表中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 各岗位的男性、女性录用比例都接近(二者之差的绝对值不大于
各岗位的男性、女性录用比例都接近(二者之差的绝对值不大于![]() ),但男性的总录用比例却明显高于女性的总录用比例.研究发现,若只考虑其中某四种岗位,则男性、女性的总录用比例也接近,请写出这四种岗位.(只需写出结论)
),但男性的总录用比例却明显高于女性的总录用比例.研究发现,若只考虑其中某四种岗位,则男性、女性的总录用比例也接近,请写出这四种岗位.(只需写出结论)