题目内容
已知定义在( ,3)上的两个函数
,3)上的两个函数 ,y=f(x)的图象在点A(
,y=f(x)的图象在点A( ,f(
,f( ))处的切线的斜率为
))处的切线的斜率为 ,
,
(1)求f(x)的解析式;
(2)试求实数k的最大值,使得对任意x∈( ,3),不等式f(x)≥kg(x)恒成立;
,3),不等式f(x)≥kg(x)恒成立;
(3)若x1,x2,x3∈( ,3)且3x1x2x3=2(x1x2+x2x3+x3x1),求证:
,3)且3x1x2x3=2(x1x2+x2x3+x3x1),求证: 。
。
 ,3)上的两个函数
,3)上的两个函数 ,y=f(x)的图象在点A(
,y=f(x)的图象在点A( ,f(
,f( ))处的切线的斜率为
))处的切线的斜率为 ,
,(1)求f(x)的解析式;
(2)试求实数k的最大值,使得对任意x∈(
 ,3),不等式f(x)≥kg(x)恒成立;
,3),不等式f(x)≥kg(x)恒成立;(3)若x1,x2,x3∈(
 ,3)且3x1x2x3=2(x1x2+x2x3+x3x1),求证:
,3)且3x1x2x3=2(x1x2+x2x3+x3x1),求证: 。
。 解:(1)由 及
及 ,即可求得a=2,
,即可求得a=2,
则 ;
;
(2)当 时,
时, ,
,
不等式 ,
,
令 ,x∈(
,x∈( ,3),
,3),
由于
 ,
,
当 时,h′(x)<0;当
时,h′(x)<0;当 时,h′(x)>0;当x∈(2,3)时,h′(x)<0.
时,h′(x)>0;当x∈(2,3)时,h′(x)<0.
又 ,故
,故 ,
,
于是由 得
得 ,即k的最大值为
,即k的最大值为 ;
;
(3)由(2)知, ,
,
在上式中分别令x=x1,x2,x3再三式作和即得,


 ,
,
所以有 。
。
 及
及 ,即可求得a=2,
,即可求得a=2,则
 ;
; (2)当
 时,
时, ,
,不等式
 ,
,令
 ,x∈(
,x∈( ,3),
,3), 由于

 ,
,当
 时,h′(x)<0;当
时,h′(x)<0;当 时,h′(x)>0;当x∈(2,3)时,h′(x)<0.
时,h′(x)>0;当x∈(2,3)时,h′(x)<0.又
 ,故
,故 ,
,于是由
 得
得 ,即k的最大值为
,即k的最大值为 ;
; (3)由(2)知,
 ,
,在上式中分别令x=x1,x2,x3再三式作和即得,


 ,
,所以有
 。
。 
练习册系列答案
相关题目
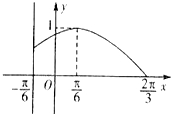 已知定义在区间[-π,
已知定义在区间[-π,