ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΈ“Ο«ΈΣΝΥΧΫΨΩΚ· ΐ![]() ΒΡ≤ΩΖ÷–‘÷ Θ§œ»Ν–±μ»γœ¬ΘΚ
ΒΡ≤ΩΖ÷–‘÷ Θ§œ»Ν–±μ»γœ¬ΘΚ
| Γ≠ | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | Γ≠ |
| Γ≠ | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.004 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | Γ≠ |
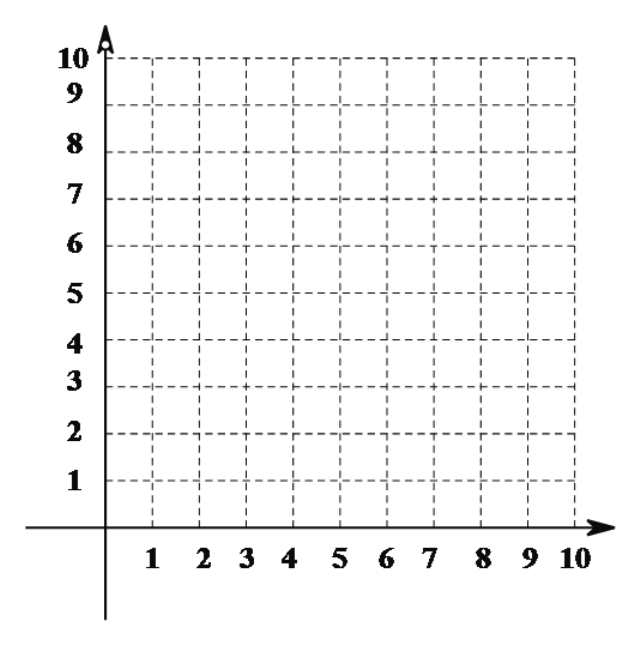
Ιέ≤λ±μ÷–![]() ÷ΒΥφ
÷ΒΥφ![]() ÷Β±δΜ·ΒΡΧΊΒψΘ§Άξ≥…“‘œ¬ΒΡΈ Χβ.
÷Β±δΜ·ΒΡΧΊΒψΘ§Άξ≥…“‘œ¬ΒΡΈ Χβ.
Ήœ»±»Ϋœ»ί“ΉΩ¥ΒΟ≥ωά¥ΘΚ¥ΥΚ· ΐ‘Ύ«χΦδ![]() …œ «ΒίΦθΒΡΘΜ
…œ «ΒίΦθΒΡΘΜ
Θ®1Θ©Κ· ΐ![]() ‘Ύ«χΦδ …œΒί‘ω
‘Ύ«χΦδ …œΒί‘ω
Β±![]() ±Θ§
±Θ§![]() = .
= .
Θ®2Θ©«κΡψΗυΨί…œΟφ–‘÷ Ής≥ω¥ΥΚ· ΐΒΡ¥σΗ≈ΆΦœώΘΜ
Θ®3Θ© ‘”ΟΚ· ΐΒΞΒς–‘ΒΡΕ®“ε÷ΛΟςΘΚΚ· ΐ![]() ‘Ύ«χΦδ
‘Ύ«χΦδ![]() …œΈΣΦθΚ· ΐ.
…œΈΣΦθΚ· ΐ.
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ,2, 4;Θ®2Θ©ΦϊΫβΈωΘΜΘ®3Θ©ΦϊΫβΈω
,2, 4;Θ®2Θ©ΦϊΫβΈωΘΜΘ®3Θ©ΦϊΫβΈω
ΓΨΫβΈωΓΩ
Θ®1Θ©”…±μΗώΒΡ ΐΨίΩ…÷Σ«χΦδ![]() …œΒίΦθΘ§«χΦδ
…œΒίΦθΘ§«χΦδ![]() …œΒί‘ωΘ§.Β±
…œΒί‘ωΘ§.Β±![]() ±Θ§”–Ήν–Γ÷Β4
±Θ§”–Ήν–Γ÷Β4
Θ®2Θ©ΗυΨί±μΗώΘ§‘ΎΉχ±ξœΒ÷–±ξ≥ωΒψΒΡΈΜ÷ΟΘ§”ΟΤΫΜ§ΒΡ«ζœΏΝ§Ϋ”ΓΘ
Θ®3Θ©ΗυΨίΒΞΒς–‘ΒΡΕ®“ε÷ΛΟςΘΚ»Έ»Γ![]() Θ§«“
Θ§«“![]() Θ§
Θ§
ΓΏ![]() ,Γύ
,Γύ![]() Θ§”÷
Θ§”÷![]() ,Γύ
,Γύ![]() Θ§
Θ§![]()
ΒΟ≥ω![]()
Θ®1Θ©Κ· ΐ![]() ‘Ύ«χΦδ
‘Ύ«χΦδ![]() …œΒί‘ω.Β±
…œΒί‘ω.Β±![]() 2 ±Θ§
2 ±Θ§![]() = 4
= 4
Θ®2Θ©

Θ®3Θ©÷ΛΟςΘΚ»Έ»Γ![]() Θ§«“
Θ§«“![]()

ΓΏ![]() ,Γύ
,Γύ![]() Θ§”÷
Θ§”÷![]() ,Γύ
,Γύ![]() Θ§
Θ§![]()
Γύ![]() Θ§Υυ“‘
Θ§Υυ“‘![]()
Υυ“‘Κ· ΐ![]() ‘Ύ«χΦδΘ®0Θ§2Θ©…œ «ΒΞΒςΒίΦθΒΡ.
‘Ύ«χΦδΘ®0Θ§2Θ©…œ «ΒΞΒςΒίΦθΒΡ.

ΝΖœΑ≤αœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ

