题目内容
已知焦点x轴上的椭圆
+
=1的离心率为
,则m的值是( )
| x2 |
| m |
| y2 |
| 2 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由于焦点x轴上的椭圆
+
=1的离心率为
,可得a2=m,b2=2.利用
=
,解出即可.
| x2 |
| m |
| y2 |
| 2 |
| 1 |
| 2 |
1-
|
| 1 |
| 2 |
解答:
解:∵焦点x轴上的椭圆
+
=1的离心率为
,
∴a2=m,b2=2.
∴
=
,
解得m=
.
故选:D.
| x2 |
| m |
| y2 |
| 2 |
| 1 |
| 2 |
∴a2=m,b2=2.
∴
1-
|
| 1 |
| 2 |
解得m=
| 8 |
| 3 |
故选:D.
点评:本题考查了椭圆的标准方程及其性质,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
设F1,F2分别为双曲线
-
=1(a>0,b>0)的左、右焦点,若在右支上存在点A,使得点F2到直线AF1的距离为2a,则该双曲线的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(1,
| ||
B、(
| ||
| C、(1,2) | ||
| D、(2,+∞) |
平面α与平面β平行的条件可以是( )
| A、α内有无穷多条直线都与β平行 |
| B、直线a∥α,a∥β且直线a不在α内,也不在β内 |
| C、直线a⊆α,直线b⊆β且a∥β,b∥α |
| D、α内的任何直线都与β平行 |
在△ABC中,已知角A=60°,边b=1,三角形的面积为
,则边c=( )
| 3 |
| A、5 | ||
B、
| ||
| C、4 | ||
| D、3 |
不等式ax2+x+b>0的解集是(-2,3),则a+b的值是( )
| A、5 | B、-5 | C、10 | D、-10 |
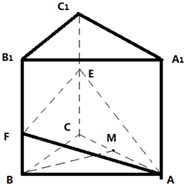 如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,点E,F分别是
如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,点E,F分别是