题目内容
某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需消耗一级子棉2吨、二级子棉1吨,生产乙种棉纱需消耗一级子棉1吨、二级子棉2吨.每1吨甲种棉纱的利润是600元,每1吨乙种棉纱的利润是900元,工厂在生产这两种棉纱的计划中要求消耗一级子棉不超过300吨、二级子棉不超过250吨.甲、乙两种棉纱应各生产多少吨,才能使利润总额最大?
思路分析:已知数据列表如下:
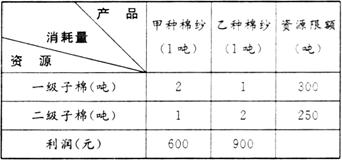
解:设生产甲、乙两种棉纱分别为x吨、y吨,那么利润总额z=600x+900y元,
线性约束条件为
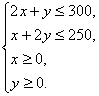
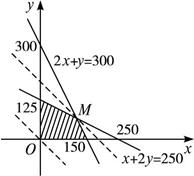
作出其可行域如下图所示.
把z=600x+900y变形为平行直线系l:y=-
x+
.
由图可知,当直线l经过可行域上的点M时,截距
最大,即z取最大值.
解方程组
得交点M(
,
).
所以应生产甲种棉纱
吨,乙种棉纱
吨.
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目