题目内容
B地在A地正东6km处,飞机保持一定高度并以一定速度向东北方向飞,地面上A、B两点高度相同,先测得飞机在A点正南仰角30°,一分钟后,又测得在B点西北仰角为45°.求飞机飞行的速度.
分析:画出示意图,设出飞机的高度,利用A点正南仰角30°,在B点西北仰角为45°,求出飞机一分钟飞行的距离,然后求出飞机飞行的速度.
解答:解:设飞机飞行高度为h,由题意画出示意图如图,
飞机保持一定高度并以一定速度向东北方向飞,地面上A、B两点高度相同,先测得飞机在A点正南仰角30°,
所以AC=
=
h.∴AE=
h,CE=
h
一分钟后,又测得在B点西北仰角为45°,
∴OB=
=h,
∴OE=h,EB=
h,
所以由AE+EB=6,(
+
)h=6,
h=6(
-
),OC=
h+h,
所以飞机飞行的速度:
=
=60(
-
) (
+1)=60(2
-
),(km/h).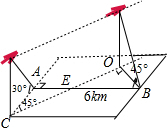
飞机保持一定高度并以一定速度向东北方向飞,地面上A、B两点高度相同,先测得飞机在A点正南仰角30°,
所以AC=
| h |
| tan30° |
| 3 |
| 3 |
| 6 |
一分钟后,又测得在B点西北仰角为45°,
∴OB=
| h |
| tan45° |
∴OE=h,EB=
| 2 |
所以由AE+EB=6,(
| 3 |
| 2 |
h=6(
| 3 |
| 2 |
| 6 |
所以飞机飞行的速度:
| OC |
| t |
(
| ||
|
| 3 |
| 2 |
| 6 |
| 2 |
| 3 |

点评:本题考查空间图形的画法,分析问题解决问题的能力,方位角的应用以及三角形的解法,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
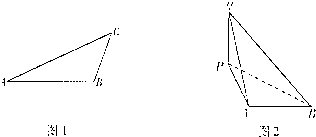 某飞船返回仓顺利返回地球后,为了及时救出航天员,地面指挥中心在返回仓预计到达的区域内安排了三个救援中心(如图1分别记为A,B,C),B地在A地正东方向上,两地相距6km; C地在B地北偏东30°方向上,两地相距4km,假设P为航天员着陆点,某一时刻A救援中心接到从P点发出的求救信号,经过4s后,B、C两个救援中心也同时接收到这一信号,已知该信号的传播速度为1km/s.
某飞船返回仓顺利返回地球后,为了及时救出航天员,地面指挥中心在返回仓预计到达的区域内安排了三个救援中心(如图1分别记为A,B,C),B地在A地正东方向上,两地相距6km; C地在B地北偏东30°方向上,两地相距4km,假设P为航天员着陆点,某一时刻A救援中心接到从P点发出的求救信号,经过4s后,B、C两个救援中心也同时接收到这一信号,已知该信号的传播速度为1km/s.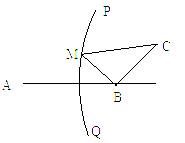 如图,B地在A地正东方向6km处,C地在
如图,B地在A地正东方向6km处,C地在