题目内容
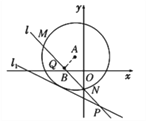
【题目】如图，已知以点A(－1,2)为圆心的圆与直线l1：x＋2y＋7＝0相切．过点B(－2,0)的动直线l与圆A相交于M，N两点，Q是MN的中点，直线l与l1相交于点P.
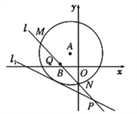
（1）求圆A的方程；
（2）当|MN|＝2
时，求直线l的方程．
【答案】(1) (x＋1)2＋(y－2)2＝20;(2) x＝－2或3x－4y＋6＝0.
【解析】试题分析：（1）利用圆心到切线的距离等于半径求得
；（2）先检验当直线斜率不存在时 
符合题意；当直线斜率存在是，设其方程为： 
，再利用点到直线的距离公式和弦长公式，即可求得
，从而求得另一条直线.
试题解析：(1)设圆A的半径为R.
由于圆A与直线l1：x＋2y＋7＝0相切，
∴R＝
＝2
.
∴圆A的方程为(x＋1)2＋(y－2)2＝20.
(2)①当直线l与x轴垂直时，易知x＝－2符合题意；
②当直线l的斜率存在时，设直线l的方程为y＝k(x＋2)．
即kx－y＋2k＝0.
连接AQ，则AQ⊥MN.
∵|MN|＝2
，∴|AQ|＝
＝1，
则由|AQ|＝
＝1，
得k＝
，∴直线l：3x－4y＋6＝0.
故直线l的方程为x＝－2或3x－4y＋6＝0.
练习册系列答案
同步练习强化拓展系列答案
相关题目
【题目】已知
三个班共有学生100人，为调查他们的体育锻炼情况，通过分层抽样获取了部分学生一周的锻炼时间，数据如下表（单位：小时）.
| 6 |
| 7 | |
| 6 | 7 | 8 | |
| 5 | 6 | 7 | 8 |
（1）试估计
班学生人数；
（2）从
班和
班抽出来的学生中各选一名，记班选出的学生为甲，班选出的学生为乙，求甲的锻炼时间大于乙的锻炼时间的概率.
