题目内容
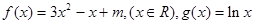
(1)若函数 f(x)与 g(x)的图像在 x=x0处的切线平行,求x0的值
(2)当曲线
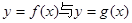 有公共切线时,求函数
有公共切线时,求函数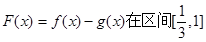 上的最值
上的最值(1)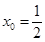 ;(2)
;(2)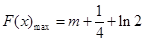
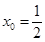 ;(2)
;(2)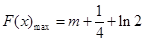
本试题主要考查了导数在研究函数中的运用。
(1)因为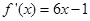 ,
,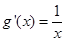 ,则
,则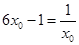 ,即
,即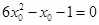 ,从而得到点的坐标。
,从而得到点的坐标。
(2)由(1)得切点横坐标为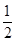 ,∴
,∴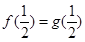 ,∴
,∴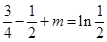 ∴
∴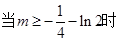 ,
,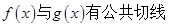 ,
,
然后构造函数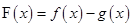 ,利用导数来排尿的尼姑单调性得到最值证明不等式成立。
,利用导数来排尿的尼姑单调性得到最值证明不等式成立。
解:(1)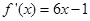 ,
,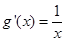 ,则
,则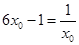 ,即
,即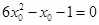
解得,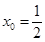 或
或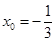 (舍去)
(舍去)
(2)由(1)得切点横坐标为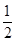 ,
,
∴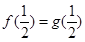 ,∴
,∴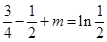
∴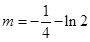 ,
,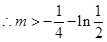 时
时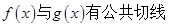
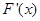
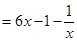
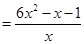
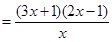
则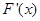 与
与 的变化如下表
的变化如下表
又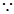
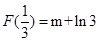
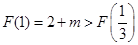
∴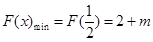 ,
,
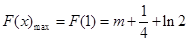 .
.
(1)因为
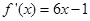 ,
,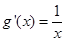 ,则
,则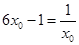 ,即
,即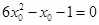 ,从而得到点的坐标。
,从而得到点的坐标。(2)由(1)得切点横坐标为
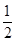 ,∴
,∴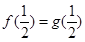 ,∴
,∴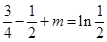 ∴
∴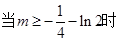 ,
,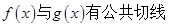 ,
,然后构造函数
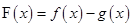 ,利用导数来排尿的尼姑单调性得到最值证明不等式成立。
,利用导数来排尿的尼姑单调性得到最值证明不等式成立。解:(1)
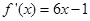 ,
,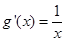 ,则
,则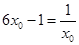 ,即
,即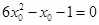
解得,
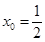 或
或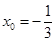 (舍去)
(舍去)(2)由(1)得切点横坐标为
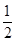 ,
,∴
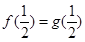 ,∴
,∴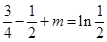
∴
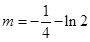 ,
,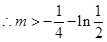 时
时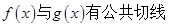
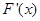
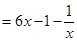
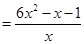
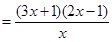
则
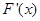 与
与 的变化如下表
的变化如下表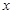 | 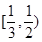 | 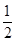 | 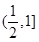 |
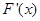 | - | 0 | + |
 | ↘ | 极小值 | ↗ |
又
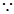
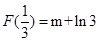
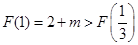
∴
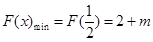 ,
,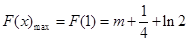 .
.
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
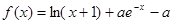 ,
,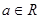 .
.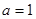 时,证明
时,证明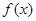 在
在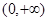 是增函数;
是增函数;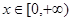 ,
,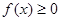 ,求
,求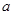 的取值范围.
的取值范围.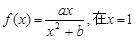 处取得极值为2.
处取得极值为2.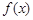 的解析式;
的解析式;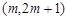 上为增函数,求实数m的取值范围;
上为增函数,求实数m的取值范围;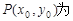
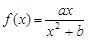 图象上的任意一点,直线l与
图象上的任意一点,直线l与 的图象相切于点P,求直线l的斜率的取值范围.
的图象相切于点P,求直线l的斜率的取值范围.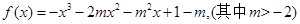 的图像在
的图像在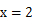 处的切线与直线
处的切线与直线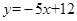 平行。
平行。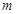 的直线;
的直线;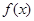 在区间
在区间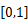 上的最小值;
上的最小值;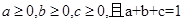 ,利用结论(2)证明:
,利用结论(2)证明: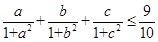
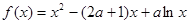
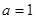 时, 求函数
时, 求函数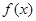 的单调增区间;
的单调增区间;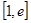 上的最小值;
上的最小值;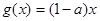 ,若存在
,若存在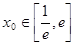 ,使得
,使得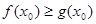 成立,求实数
成立,求实数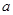 的取值范围.
的取值范围.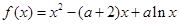 ,其中
,其中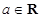 .
.  的图象在点
的图象在点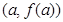 处的切线与直线
处的切线与直线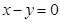 平行,求实数
平行,求实数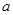 的值;
的值;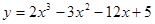 在[0,3]上的最大值,最小值分别是 ( )
在[0,3]上的最大值,最小值分别是 ( )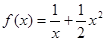 ,存在
,存在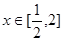 ,使得
,使得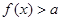 成立,则实数
成立,则实数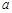 的取值范围是( )
的取值范围是( )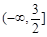
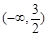

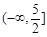
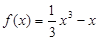 在
在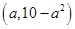 上有最小值,则实数
上有最小值,则实数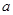 的取值范围是 .
的取值范围是 .