题目内容
(本题16分)在平面直角坐标系 中,
中, 是抛物线
是抛物线 的焦点,
的焦点, 是抛物线
是抛物线 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过 三点的圆的圆心为
三点的圆的圆心为 ,点
,点 到抛物线
到抛物线 的准线的距离为
的准线的距离为 .
.
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)是否存在点 ,使得直线
,使得直线 与抛物线
与抛物线 相切于点
相切于点 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(Ⅲ)若点 的横坐标为
的横坐标为 ,直线
,直线 与抛物线
与抛物线 有两个不同的交点
有两个不同的交点 ,
, 与圆
与圆 有两个不同的交点
有两个不同的交点 ,求当
,求当 时,
时, 的最小值.
的最小值.
【答案】
(1) ,(2)存在,
,(2)存在, ,
, (3)
最小值
(3)
最小值
【解析】利用抛物线的几何性质、圆的方程以及直线与圆锥曲线的位置关系求解。
试题分析:
(1)由题意,知 ,圆心
,圆心 在线段
在线段 的中垂线
的中垂线 上,抛物线准线方程为
上,抛物线准线方程为 ,所以
,所以 ,得,
,得, ,抛物线方程为
,抛物线方程为 ……………………….4分
……………………….4分
(2)假设存在点 满足条件,抛物线
满足条件,抛物线 在点
在点 处的切线斜率为
处的切线斜率为 ,所以,直线
,所以,直线 ,令
,令 ,得
,得 ,故
,故 ,
,
又 ,得,
,得, ,由
,由 ,解得
,解得 ,
, 满足条件。…………………………………………8分
满足条件。…………………………………………8分
(3)当 时,由(2)知
时,由(2)知 ,圆
,圆 的半径
的半径 ,
,
圆 设
设 ,
, 由
由 ,整理得
,整理得
 ,
, ,
,
设 ,
, 由
由 ,整理得
,整理得 ,
,
 ,令
,令 ,
, ,
, ,
,
 ,
,
 ,当
,当 时,
时,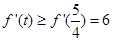 ,
, 在
在 递增,故当
递增,故当 ,即
,即 时,有最小值
时,有最小值 ……………………………………………………………….16分
……………………………………………………………….16分
考点:本题主要考查了抛物线的几何性质、圆的方程以及直线与圆锥曲线的位置关系等,综合考查了学生的运算求解能力和推理论证能力。
点评:解决此题的关键是掌握抛物线的几何性质、圆的方程以及直线与圆锥曲线的位置关系等知识以及较强的运算求解能力和推理论证能力,难度很大。

练习册系列答案
相关题目
 =2
=2 =2.
=2. ;
; ∥平面
∥平面 ;
;
 的体积
的体积 .
.
