题目内容

已知⊙O中，AB=AC，D是BC延长线上一点，AD交⊙O于E.

求证：AB2=AD·AE.

图2-1-11

思路分析：由欲证的乘积式写出比例式，找到应该证明的相似的三角形，利用同弧所对的圆周角相等的性质进行证明.

证明：∵AB=AC,∴=AC.∴∠ABD=∠AEB.

在△ABE与△ADB中,

∴△ABE∽△ADB.∴,即AB2=AD·AE.

    深化升华 在圆当中证明比例式或等积式时，通常利用两角相等加以说明，这当中使用最多的就是利用圆周角转移角的位置，产生相似关系.

练习册系列答案
相关题目
已知△ABC中，
AB
=
a
，
AC
=
b
．对于平面ABC上任意一点O，动点P满足
OP
=
OA
+λ
a
+λ
b
，λ∈[0，+∞）．试问动点P的轨迹是否过某一个定点？说明理由．
已知△ABC中，AB=AC=3，cos∠ABC=
2
3
．若圆O的圆心在边BC上，且与AB和AC所在的直线都相切，则圆O的半径为（　　）
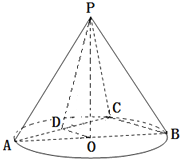精英家教网如图，在体积为
2
3
π的圆锥PO中，已知⊙O的直径AB=2，C是
AB
的中点，D是弦AC的中点．
（1）指出二面角D-PO-A的平面角，并求出它的大小；
（2）求异面直线PD与BC所成的角的正切值．
已知△ABC中，AB=AC=3，cos∠ABC=
2
3
．若圆O的圆心在边BC上，且与AB和AC所在的直线都相切，则圆O的半径为（　　）
A．
3
5
2
B．
2
5
3
C．
3
D．
2
3
3
已知△ABC中，
AB
=
a
，
AC
=
b
．对于平面ABC上任意一点O，动点P满足
OP
=
OA
+λ
a
+λ
b
，λ∈[0，+∞）．试问动点P的轨迹是否过某一个定点？说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网