题目内容

15．已知集合A={-1，2，3，4，5}，B={x|x＜m}，若A∩B={-1}，则实数m的值可以是（　　）
A．-1B．2C．3D．4

分析 根据集合的交集的运算求出m的范围，即可得到答案．

解答 解：集合A={-1，2，3，4，5}，B={x|x＜m}，A∩B={-1}，
∴-1＜m≤2，
∴实数m的值可以是0，1，2，
故选：B．

点评 本题以集合为载体，考查集合的运算，解题的关键是根据A∩B={-3}，确定m的范围，属于基础题．

练习册系列答案
相关题目
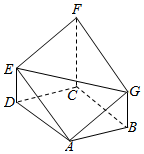5．在如图所示的多面体ABCDEFG中，面ABCD是边长为2的菱形，∠BAD=120°，DE∥CF∥BG，CF⊥面ABCD，AG∥EF，且CF=2 BG=4．
（I）证明：EG∥平面ABCD；
（Ⅱ）求直线CF与平面AEG所成角的正弦值．
6．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-4y2=1（a＞0）的右顶点到其一条渐近线的距离等于$\frac{\sqrt{3}}{4}$，抛物线E：y2=2px的焦点与双曲线C的右焦点重合，则抛物线E上的动点M到直线l1：4x-3y+6=0和l2：x=-1的距离之和的最小值为（　　）
A．1B．2C．3D．4
3．在△ABC中，角A，B，C所对边分别为a，b，c，已知$\frac{sinA}{sinB+sinC}=1-\frac{a-b}{a-c}$．
（Ⅰ）若b=$\sqrt{3}$，当△ABC周长取最大值时，求△ABC的面积；
（Ⅱ）设$\overrightarrow m=（{sinA，1}），\overrightarrow n=（{6cosB，cos2A}），求\overrightarrow m•\overrightarrow n$的取值范围．
10．已知a，b是不全为零的实数，函数f（x）=3ax2+2bx-（a+b）（a，b均为实数）
（Ⅰ）若a=1，且对一切b∈（1，2）恒有f（x）＞3x2+b2，求x的取值范围；
（Ⅱ）求证：函数f（x）在（0，1）内一定有零点．
20．若不等式x2+ax+1≥0对一切x∈（0，1]恒成立，则a的最小值为（　　）
A．0B．-2C．-$\frac{5}{2}$D．-3
7．直三棱柱ABC-A1B1C1中的侧棱长为4cm，在底面△ABC中，AC=BC=2cm，∠ACB=90°，E为AB的中点，CF⊥AB1垂足为F
（Ⅰ）求证CE⊥AB1；
（Ⅱ）求CE与AB1的距离；
（Ⅲ）求截面AB1C与侧面ABB1A1所成二面角C-AB1-B的正切值；
（Ⅳ）求三棱锥C-AEF的体积．
4．某单位在对一个长800m、宽600m的草坪进行绿化时，是这样想的：中间为矩形绿草坪，四周是等宽的花坛，如图所示，若要保证绿草坪的面积不小于总面积的二分之一．试确定花坛宽度的取值范围．
5．在等比数列{an}中，公比q≠1；
（1）已知a1，q，n，求a4与Sn；
（2）已知an，q，n，求Sn；
（3）已知q，Sn，n，求a1与an．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网