题目内容
求证:(1)若射影定理成立,则勾股定理成立;(2)若勾股定理成立,则射影定理成立.
图
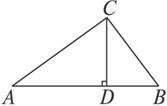
证明:如图,Rt△ABC中,CD为斜边上的高.
(1)由射影定理AC2=AD·AB,BC2=BD·AB,
∴AC2+BC2=AD·AB+BD·AB
=(AD+BD)·AB
=AB2,
即勾股定理成立.
(2)∵AB=AD+BD,
∴AB2=(AD+BD)2=AD2+BD2+2AD·BD.
∴AB2-AD2-BD2=2AD·BD.
∴AC2+BC2-AD2-BD2=2AD·BD.
∴(AC2-AD2)+(BC2-BD2)=2AD·BD.
∴CD2+CD2=2AD·BD.
∴CD2=AD·BD.①
∵AC2=CD2+AD2
=AD·BD+AD2
=AD(BD+AD)
=AD·AB,②
同理,BC2=BD·AB.③
由①②③说明若勾股定理成立,则射影定理成立.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
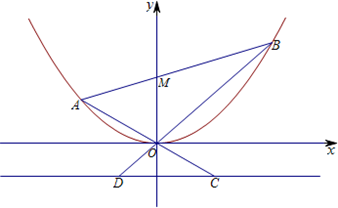 已知抛物线E:x2=4y,直线l过点M(0,2)且与抛物线交于A、B两点,直线OA、OB分别与抛物线的准线l0交于C、D.
已知抛物线E:x2=4y,直线l过点M(0,2)且与抛物线交于A、B两点,直线OA、OB分别与抛物线的准线l0交于C、D.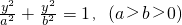 的上、下焦点及左、右顶点均在圆O:x2+y2=1上.
的上、下焦点及左、右顶点均在圆O:x2+y2=1上.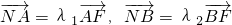 ,求证:λ1+λ2为定值.
,求证:λ1+λ2为定值.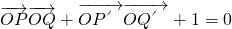 ,若点S满足:
,若点S满足: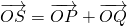 ,证明:点S在椭圆C2上.
,证明:点S在椭圆C2上. 的上、下焦点及左、右顶点均在圆O:x2+y2=1上,
的上、下焦点及左、右顶点均在圆O:x2+y2=1上, ,求证:λ1+λ2为定值;
,求证:λ1+λ2为定值; ,若点S满足:
,若点S满足: ,证明:点S在椭圆C2上。
,证明:点S在椭圆C2上。  的上、下焦点及左、右顶点均在圆O:x2+y2=1上.
的上、下焦点及左、右顶点均在圆O:x2+y2=1上. ,求证:λ1+λ2为定值.
,求证:λ1+λ2为定值. ,若点S满足:
,若点S满足: ,证明:点S在椭圆C2上.
,证明:点S在椭圆C2上.