题目内容
已知抛物线C1：y2=2px（p＞0）的焦点F以及椭圆C2：
的上、下焦点及左、右顶点均在圆O：x2+y2=1上，
(Ⅰ)求抛物线C1和椭圆C2的标准方程；
(Ⅱ)过点F的直线交抛物线C1于A、B两不同点，交y轴于点N，已知
，求证：λ1+λ2为定值；
(Ⅲ)直线l交椭圆C2于P、Q两不同点，P、Q在x轴的射影分别为P′、Q′，
，若点S满足：
，证明：点S在椭圆C2上。
的上、下焦点及左、右顶点均在圆O：x2+y2=1上，(Ⅰ)求抛物线C1和椭圆C2的标准方程；
(Ⅱ)过点F的直线交抛物线C1于A、B两不同点，交y轴于点N，已知
，求证：λ1+λ2为定值；(Ⅲ)直线l交椭圆C2于P、Q两不同点，P、Q在x轴的射影分别为P′、Q′，
，若点S满足：，证明：点S在椭圆C2上。 解：（Ⅰ）由C1：y2=2px（p＞0）的焦点
在圆O：x2+y2=1上得：
，∴p=2，
所以抛物线C1：
，
同理由椭圆C2：
的上、下焦点（0，c），（0，-c）及左、右顶点（-b，0），（b，0）均在圆O：x2+y2=1上可解得：b=c=1，∴
，
得椭圆C2：
；
总之，抛物线C1：
、椭圆C2：
。
（Ⅱ）设直线AB的方程为y=k（x-1），
，则N（0，-k），
联立方程组
消去y得：
，
，
故
，
由
得，
，
整理得，
，
∴
。
（Ⅲ）设
，∴
，则
，
由
得：
，（1）
，（2）
，（3）
由（1）+（2）+（3）得：
，
所以
满足椭圆C2的方程，命题得证。
在圆O：x2+y2=1上得：，∴p=2，所以抛物线C1：
，同理由椭圆C2：
的上、下焦点（0，c），（0，-c）及左、右顶点（-b，0），（b，0）均在圆O：x2+y2=1上可解得：b=c=1，∴，得椭圆C2：
；总之，抛物线C1：
、椭圆C2：。（Ⅱ）设直线AB的方程为y=k（x-1），
，则N（0，-k），联立方程组
消去y得：，，故
，由
得，， 整理得，
，∴
。（Ⅲ）设
，∴，则，由
得：，（1），（2），（3） 由（1）+（2）+（3）得：
，所以
满足椭圆C2的方程，命题得证。
练习册系列答案
习题精选系列答案
相关题目
（2012•河北模拟）已知抛物线C1：y2=2px和圆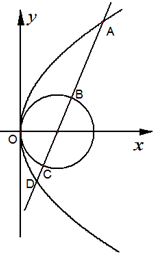
已知抛物线C1：y2=4x，圆C2：（x-1）2+y2=1，过抛物线焦点F的直线l交C1于A，D两点（点A在x轴上方），直线l交C2于B，C两点（点B在x轴上方）．