题目内容
如图,在四棱锥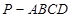 中,底面为直角梯形,
中,底面为直角梯形,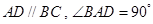 ,
,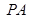 垂直于底面
垂直于底面 ,
,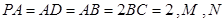 分别为
分别为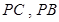 的中点.
的中点.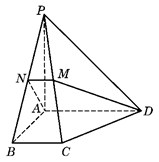
(1)求证: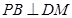 ;
;
(2)求点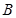 到平面
到平面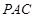 的距离.
的距离.
(1)证明见解析;(2) .
.
解析试题分析:(1)要证两直线垂直,一般是证一条直线与过另一条直线的某个平面垂直,例如能否证明 垂直于过
垂直于过 的平面
的平面 ,下面就是要在平面
,下面就是要在平面 内找两条与
内找两条与 垂直的直线,从题寻找垂直,
垂直的直线,从题寻找垂直,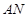 是等腰
是等腰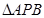 的底边上的中线,与
的底边上的中线,与 是垂直的,另一条是直线
是垂直的,另一条是直线 垂直于平面
垂直于平面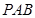 ,当然也垂直于直线
,当然也垂直于直线 ,得证;(2)求点
,得证;(2)求点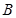 到平面
到平面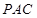 距离,关键是过点
距离,关键是过点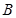 作出平面
作出平面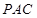 的垂线,这一点在本题中还是委容易的,因为平面
的垂线,这一点在本题中还是委容易的,因为平面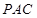
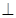 平面
平面 ,故只要在平面
,故只要在平面 内过
内过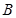 作
作 的垂线,这条垂线也我们要求作的平面的垂线,另外体积法在本题中也可采用.
的垂线,这条垂线也我们要求作的平面的垂线,另外体积法在本题中也可采用.
试题解析:(1)因为N是PB的中点,PA=AB,
所以AN⊥PB,因为AD⊥面PAB,所以AD⊥PB,又因为AD∩AN=A
从而PB⊥平面ADMN,因为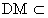 平面ADMN,
平面ADMN,
所以PB⊥DM. 7′
(2) 连接AC,过B作BH⊥AC,因为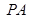 ⊥底面
⊥底面 ,
,
所以平面PAB⊥底面 ,所以BH是点B到平面PAC的距离.
,所以BH是点B到平面PAC的距离.
在直角三角形ABC中,BH= 14′
14′
考点:(1)空间两直线垂直;(2)点到平面的距离.

练习册系列答案
相关题目
 ,
, ,DC=1,AB=2,PA⊥平面ABCD,PA=1.
,DC=1,AB=2,PA⊥平面ABCD,PA=1.
 的底面
的底面 为矩形,且
为矩形,且 ,
,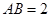 ,
, ,
,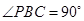 ,
,
 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD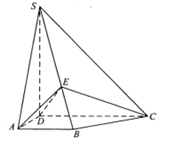
 ;
; ,当平面EDC
,当平面EDC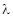 的值;
的值;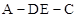 的大小.
的大小. 中,
中,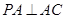 ,
,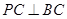 ,
, 为
为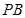 的中点,
的中点, 为
为 的中点,且
的中点,且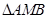 为正三角形.
为正三角形.
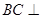 平面
平面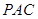 ;
;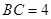 ,
,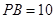 ,求点
,求点 到平面
到平面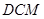 的距离.
的距离.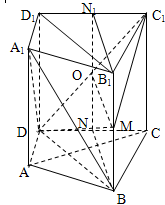
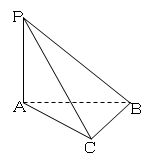
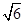 ,PC与侧面APB所成角的余弦值为
,PC与侧面APB所成角的余弦值为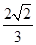 ,PB与底面ABC成60°角,求二面角B―PC―A的大小。
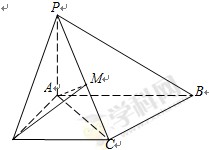
,PB与底面ABC成60°角,求二面角B―PC―A的大小。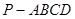 中,底面
中,底面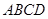 是直角梯形,
是直角梯形,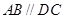 ,
,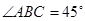 ,
,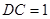 ,
,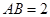 ,
,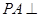 平面
平面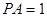 .
. 
 平面
平面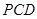 ;
; 平面
平面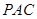 ;
; 是
是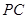 的中点,求三棱锥
的中点,求三棱锥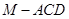 的体积.
的体积.