题目内容
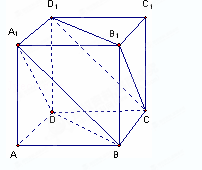
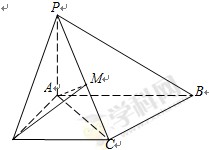
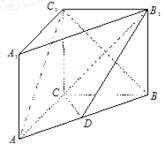
如图,已知四棱锥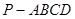 中,底面
中,底面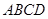 是直角梯形,
是直角梯形,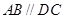 ,
,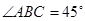 ,
,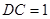 ,
,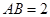 ,
,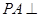 平面
平面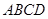 ,
,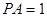 .
. 
(Ⅰ)求证: 平面
平面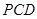 ;
;
(Ⅱ)求证: 平面
平面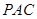 ;
;
(Ⅲ)若 是
是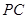 的中点,求三棱锥
的中点,求三棱锥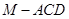 的体积.
的体积.
证明过程详见试题解析.
解析试题分析:(Ⅰ)要证明直线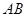 与平面
与平面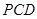 平行,就是要证明直线
平行,就是要证明直线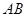 与平面
与平面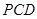 内一条直线平行,根据题意显然直线
内一条直线平行,根据题意显然直线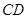 满足要求. (Ⅱ)要证明
满足要求. (Ⅱ)要证明 平面
平面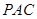 ,就是要证明直线
,就是要证明直线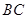 与平面
与平面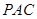 内两条相交直线垂直.根据题意
内两条相交直线垂直.根据题意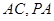 符合要求.(Ⅲ)要求三棱锥
符合要求.(Ⅲ)要求三棱锥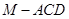 的体积,就是要求出
的体积,就是要求出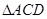 的面积以及三棱锥
的面积以及三棱锥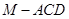 的高.
的高.
试题解析:(Ⅰ)证明: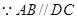 ,且
,且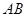
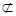 平面
平面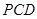
∴ 平面
平面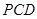 .
.
(Ⅱ)证明:在直角梯形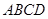 中,过
中,过 作
作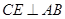 于点
于点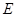 ,则四边形
,则四边形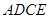 为矩形
为矩形
∴ ,又
,又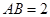 ,∴
,∴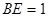 ,在Rt△
,在Rt△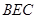 中,
中,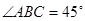 ,
,
∴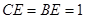 ,
,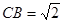
∴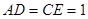 ,则
,则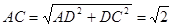 ,
,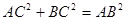
∴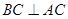
又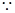
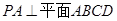 ∴
∴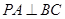
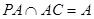 ∴
∴ 平面
平面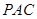
(Ⅲ)∵ 是
是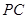 中点,
中点,
∴ 到面
到面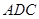 的距离是
的距离是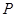 到面
到面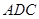 距离的一半
距离的一半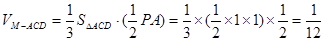
考点:线面平行,线面垂直,三棱锥体积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
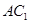 ∥平面
∥平面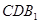 ;
;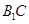 所成角的余弦值.
所成角的余弦值.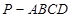 中,底面为直角梯形,
中,底面为直角梯形,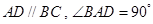 ,
,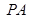 垂直于底面
垂直于底面 ,
,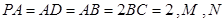 分别为
分别为 的中点.
的中点.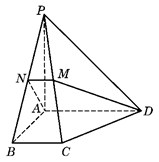
 ;
; 到平面
到平面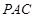 的距离.
的距离.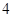 的正方形
的正方形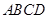 和等腰直角三角形
和等腰直角三角形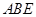 按图拼为新的几何图形,
按图拼为新的几何图形,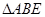 中,
中,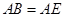 ,连结
,连结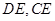 ,若
,若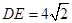 ,
,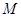 为
为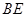 中点
中点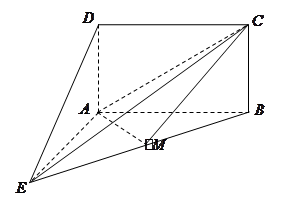
 与
与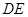 所成角的大小;
所成角的大小;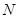 为
为 中点,证明:
中点,证明: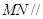 平面
平面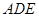 ;
;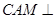 平面
平面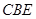
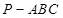 中,
中,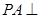 平面
平面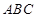 ,
, ,
, 为侧棱
为侧棱 上一点,它的正(主)视图和侧(左)视图如图所示.
上一点,它的正(主)视图和侧(左)视图如图所示.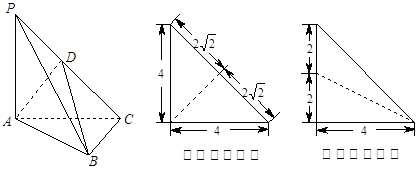
 平面
平面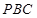 ;
;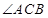 的平分线上确定一点
的平分线上确定一点 ,使得
,使得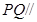 平面
平面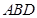 ,并求此时
,并求此时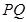 的长.
的长.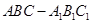 中,侧面
中,侧面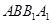 ,
,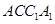 均为正方形,∠
均为正方形,∠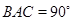 ,点
,点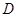 是棱
是棱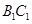 的中点.
的中点.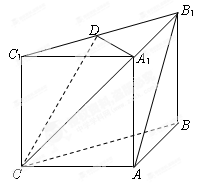
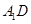 ⊥平面
⊥平面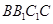 ;
;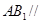 平面
平面 ;
;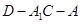 的余弦值.
的余弦值.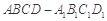 ,中,
,中,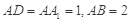 ,点
,点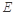 在棱AB上移动.
在棱AB上移动.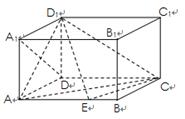
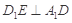 ;
; 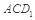 的距离;
的距离;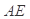 等于何值时,二面角
等于何值时,二面角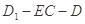 的大小为
的大小为
 中,底面
中,底面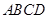 为菱形,
为菱形,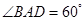 ,
,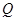 为
为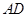 的中点.
的中点.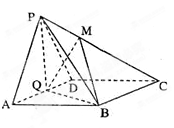
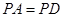 ,求证:平面
,求证:平面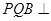 平面
平面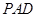 ;
;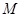 在线段
在线段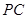 上,
上,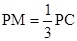 ,若平面
,若平面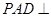 平面
平面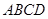 ,且
,且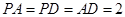 ,求二面角
,求二面角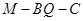 的大小.
的大小.