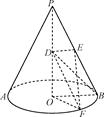
题目内容
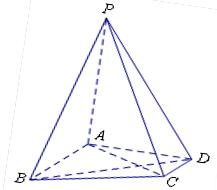
已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿直线BD将△BCD翻折成△BC D,使得平面BC
D,使得平面BC D
D 平面ABD.
平面ABD.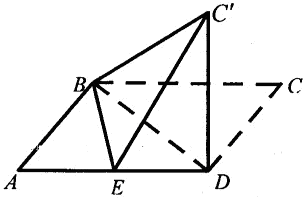
(1)求证:C'D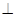 平面ABD;
平面ABD;
(2)求直线BD与平面BEC'所成角的正弦值.
(1)证明:见解析;(2)直线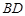 与平面
与平面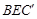 所成角的正弦值为
所成角的正弦值为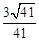 .
.
解析试题分析:(1)注意到平行四边形 中,
中,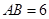 ,
,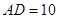 ,
,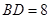 ,
,
沿直线 将△
将△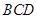 翻折成△
翻折成△ 后
后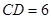 ,
,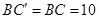 ,
,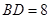 ,
,
由给定了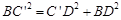 ,得
,得 .再根据平面
.再根据平面 ⊥平面
⊥平面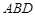 ,平面
,平面
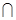 平面
平面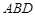 即得证;
即得证;
(2)由(1)知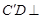 平面
平面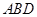 ,且
,且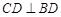 ,因此,可以
,因此,可以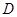 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系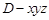 .
.
确定平面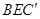 法向量为
法向量为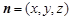 ,
,
设直线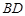 与平面
与平面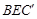 所成角为
所成角为 ,即得所求.
,即得所求.
试题解析:(1)平行四边形 中,
中,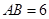 ,
,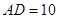 ,
,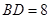 ,
,
沿直线 将△
将△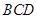 翻折成△
翻折成△
可知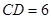 ,
,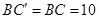 ,
,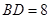 ,
,
即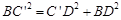 ,
, . 2分
. 2分
∵平面 ⊥平面
⊥平面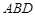 ,平面
,平面
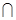 平面
平面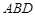 ,
,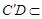 平面
平面 ,∴
,∴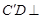 平面
平面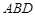 . 5分
. 5分
(2)由(1)知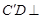 平面
平面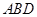 ,且
,且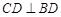 ,
,
如图,以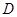 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系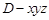 . 6分
. 6分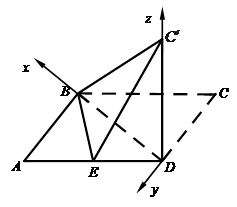
则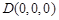 ,
,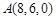 ,
,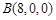 ,
,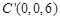 .
.
∵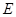 是线段
是线段 的中点,
的中点,
∴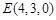 ,
,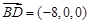 .
.
在平面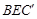 中,
中,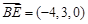 ,
,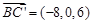 ,
,
设平面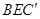 法向量为
法向量为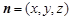 ,
,
∴ 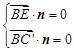 ,即
,即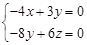 ,
,
令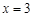 ,得
,得
练习册系列答案
相关题目
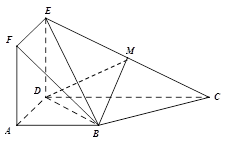
 与梯形
与梯形 所在的平面互相垂直,
所在的平面互相垂直,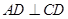 ,
, ∥
∥ ,
,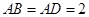 ,
,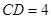 ,
,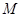 为
为 的中点.
的中点.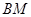 ∥平面
∥平面 平面
平面 ;
;
 为平行四边形,
为平行四边形, ,
,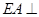 平面
平面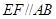 ,
,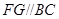 ,
,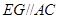 ,
,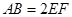 .
.
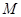 是线段
是线段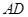 的中点,求证:
的中点,求证: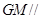 平面
平面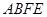 ;
;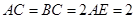 ,求二面角
,求二面角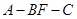 的余弦值.
的余弦值. 中,
中,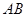 //
//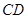 ,
,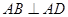 ,
,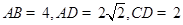 ,
,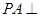 平面
平面 ,
,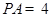 .
. 
 平面
平面 ;
;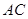 与
与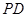 所成角的余弦值;
所成角的余弦值;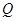 为线段
为线段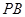 上一点,且直线
上一点,且直线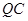 与平面
与平面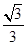 ,求
,求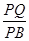 的值.
的值. 的底面为直角梯形,
的底面为直角梯形,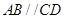 ,
,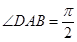 ,
,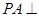 底面
底面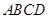 ,且
,且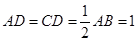 ,
, 是
是 的中点.
的中点. 平面
平面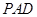 ;
; 与平面
与平面 所成的角为
所成的角为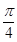 ,求二面角
,求二面角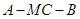 的余弦值.
的余弦值.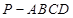 中,
中,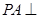 面
面 ,
,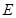 、
、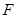 分别为
分别为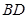 、
、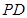 的中点,
的中点, ,
,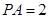 .
.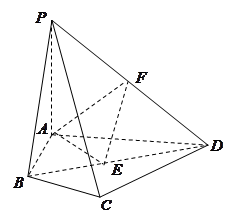
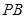 ∥面
∥面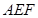 ;
;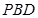 与面
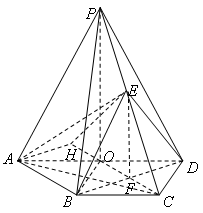
与面 中,底面
中,底面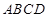 是直角梯形,
是直角梯形,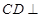 平面
平面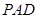 ,
,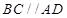 ,
, ,
,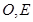 分别为
分别为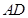 ,
,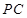 的中点,
的中点,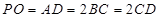 .
.
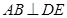 ;
;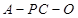 的余弦值.
的余弦值. 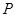 是正方形
是正方形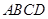 所在平面外一点,且
所在平面外一点,且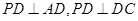 ,
,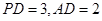 ,若
,若 、
、 分别是
分别是 、
、 的中点.
的中点.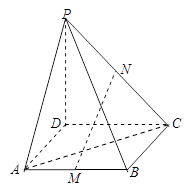
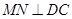 ;
;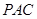 的距离.
的距离.