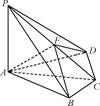
题目内容
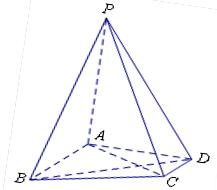
在四棱锥 中,
中,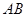 //
//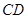 ,
,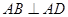 ,
,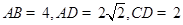 ,
,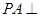 平面
平面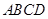 ,
,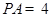 .
. 
(1)求证: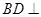 平面
平面 ;
;
(2)求异面直线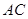 与
与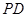 所成角的余弦值;
所成角的余弦值;
(3)设点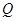 为线段
为线段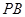 上一点,且直线
上一点,且直线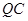 与平面
与平面 所成角的正弦值为
所成角的正弦值为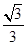 ,求
,求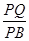 的值.
的值.
(1)见解析(2)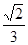 ,(3)
,(3)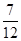
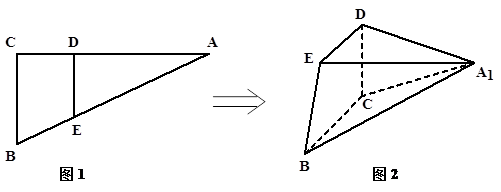
解析试题分析:(1)建立如图所示坐标系,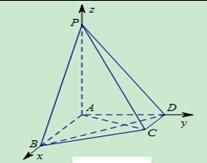
写出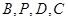 坐标,可得
坐标,可得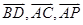 坐标,由
坐标,由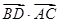 =
= ,
, =
= 知
知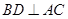 ,
,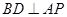 .所以
.所以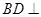 平面
平面 ;(2)由
;(2)由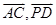 向量的夹角可知异成直线
向量的夹角可知异成直线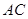 与
与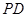 所成角;(3)
所成角;(3)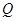 为线段
为线段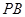 上一点,设
上一点,设 其中
其中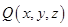 可得
可得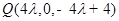 ,由直线
,由直线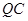 与平面
与平面 所成角的正弦值为
所成角的正弦值为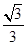 ,利用
,利用 与平面
与平面 的法向量
的法向量 夹角,可得
夹角,可得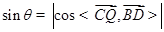 .其中
.其中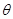 为直线
为直线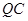 与平面
与平面 所成角.
所成角.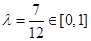 .即
.即 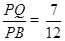 .
.
试题解析:(1)证明: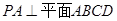 因为,
因为,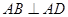 ,所以以
,所以以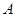 为坐标原点,
为坐标原点,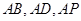 所在的直线分别为
所在的直线分别为 轴、
轴、 轴、
轴、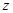 轴建立空间直角坐标系, 1分
轴建立空间直角坐标系, 1分
则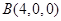 ,
,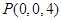 ,
,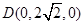 ,
,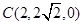 .
.
所以  ,
,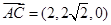 ,
,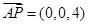 , 2分
, 2分
所以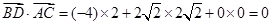 ,
,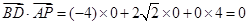 .
.
所以 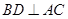 ,
,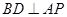 .
.
因为 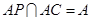 ,
,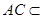 平面
平面 ,
,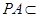 平面
平面 ,
,
所以 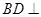 平面
平面 . 4分
. 4分
(2) 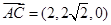 ,
,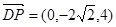 5分
5分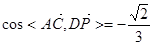
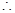 异成直线
异成直线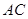 与
与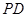 所成角的余弦值
所成角的余弦值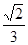 8分
8分
(3)解:设 (其中
(其中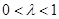 ),
),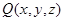 ,直线
,直线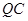 与平面
与平面 所成角为
所成角为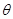 .
.
所以 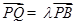 .所以
.所以 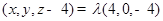 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
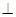 平面AEB,AE
平面AEB,AE
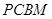 是直角梯形,∠
是直角梯形,∠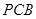 =90°,
=90°,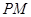 ∥
∥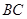 ,
,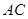 =1,∠
=1,∠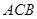 =120°,
=120°,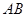 ⊥
⊥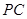 ,直线
,直线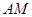 与直线
与直线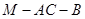 的的余弦值;
的的余弦值; 到面
到面 的距离.
的距离.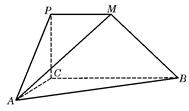
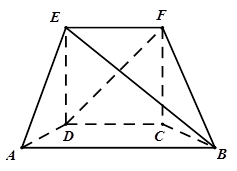
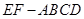 中,
中,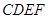 为边长为
为边长为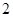 的正方形,
的正方形,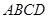 为直角梯形,
为直角梯形, ,
,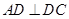 ,
,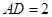 ,
, ,
,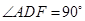 .
.
 和
和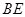 所成角的大小;
所成角的大小;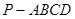 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱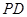 ⊥底面
⊥底面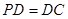 ,
,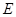 是
是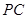 的中点,作
的中点,作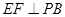 交
交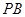 于点
于点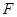 .
.
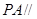 平面
平面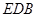 ;
;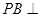 平面
平面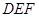 .
.
 D,使得平面BC
D,使得平面BC 平面ABD.
平面ABD.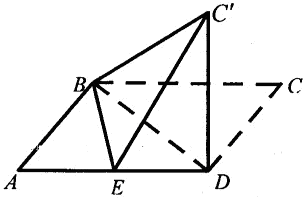
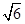 ,平面PAC⊥平面ABC,PD⊥AC于点D,AD=1,CD=3,PD=
,平面PAC⊥平面ABC,PD⊥AC于点D,AD=1,CD=3,PD= .
.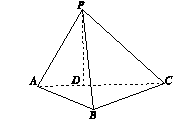
 ,F为PC的中点,AF⊥PB.
,F为PC的中点,AF⊥PB.