题目内容
已知函数![]() 在
在![]() 处取到极值2.
处取到极值2.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)设函数![]() .若对任意的
.若对任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
解: (Ⅰ)![]() (2分)
(2分)
由![]() 在
在![]() 处取到极值2,故
处取到极值2,故![]() ,
,![]() 即
即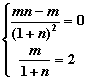 ,
,![]()
解得![]() ,经检验,此时
,经检验,此时![]() 在
在![]() 处取得极值.故
处取得极值.故![]() (4分)
(4分)
(Ⅱ)由(Ⅰ)知![]() 的定义域为R,且
的定义域为R,且![]() .故
.故![]() 为奇函数.
为奇函数.![]()
![]()
![]() >0时,
>0时,![]() >0,
>0,![]() 。当且仅当
。当且仅当![]() 时取“=”.
时取“=”.
故![]() 的值域为
的值域为![]() .从而
.从而![]() .依题意有
.依题意有![]() (7分)
(7分)
函数![]() 的定义域为
的定义域为![]() ,
, ![]() (8分)
(8分)
①当![]() 时,
时,![]() >0函数
>0函数![]() 在
在![]() 上单调递增,其最小值为
上单调递增,其最小值为![]() 合题意;
合题意;
②当![]() 时,函数
时,函数![]() 在
在![]() 上有
上有![]() ,单调递减,在
,单调递减,在![]() 上有
上有
![]() ,单调递增,所以函数
,单调递增,所以函数![]() 最小值为
最小值为![]() ,由
,由![]() ,得
,得![]() .从而知
.从而知![]() 符合题意.
符合题意.
③当![]() 时,显然函数
时,显然函数![]() 在
在![]() 上单调递减,其最小值为
上单调递减,其最小值为![]() ,不合题意(11分)综上所述,
,不合题意(11分)综上所述,![]() 的取值范围为
的取值范围为![]() (12分)
(12分)

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
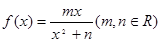 在
在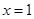 处取到极值
处取到极值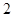
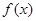 的解析式;
的解析式;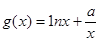 ,若对任意的
,若对任意的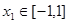 ,总存在
,总存在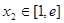 ,使得
,使得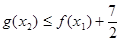 ,求实数
,求实数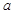 的取值范围.
的取值范围.
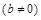 在
在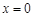 处取到极值2.
处取到极值2.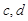 的值;
的值;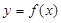 的所有切线与直线
的所有切线与直线 垂直的条数;
垂直的条数;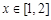 ,均存在
,均存在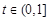 ,使得
,使得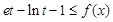 ,试求
,试求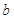 的取值范围.
的取值范围. 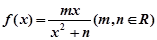 在
在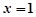 处取到极值2
处取到极值2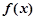 的解析式;
的解析式;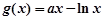 .若对任意的
.若对任意的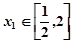 ,总存在唯一的
,总存在唯一的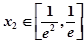 ,使得
,使得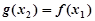 ,求实数
,求实数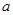 的取值范围.
的取值范围.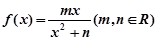 在
在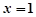 处取到极值2
处取到极值2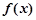 的解析式;
的解析式;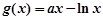 .若对任意的
.若对任意的 ,总存在唯一的
,总存在唯一的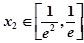 ,使得
,使得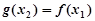 ,求实数
,求实数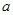 的取值范围.
的取值范围.