Question

（本小题满分12分）

已知函数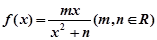在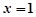处取到极值2

（Ⅰ）求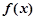的解析式；

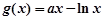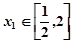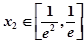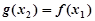（Ⅱ）设函数.若对任意的，总存在唯一的，使得，求实数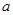的取值范围.

 

请考生在第22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分.

 

Answer 1

【答案】

解: （Ⅰ）                     (2分)

由在处取到极值2，故，即,

解得，经检验，此时在处取得极值.故     (4分)

（Ⅱ）由（Ⅰ）知，故在上单调递增，

在上单调递减,由 ，故的值域为   (6分)

依题意，记

（ⅰ）当时，，在上单调递减，依题意由得，

故此时                                                        (8分)

（ⅱ）当时，>>当时，<，当时，>

依题意由，得，即.与矛盾           (10分)

（ⅲ）当>时，<，此时>，在上单调递增,依题意得

  即此不等式组无解(11分).综上，所求取值范围为(12分)  

【解析】略