题目内容
已知在直角坐标平面内,以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系,点 的极坐标是
的极坐标是 ,曲线C的极坐标方程为
,曲线C的极坐标方程为 .
.
(I)求点 的直角坐标和曲线C的直角坐标方程;
的直角坐标和曲线C的直角坐标方程;
(II)若经过点 的直线
的直线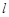 与曲线C交于A、B两点,求
与曲线C交于A、B两点,求 的最小值.
的最小值.
(1)  ,
, 
(2) 当 时,
时, 取得最小值3.
取得最小值3.
解析试题分析:解:(I)点 的直角坐标是
的直角坐标是 , (2分)
, (2分)
∵ ,∴
,∴ ,即
,即 , (5分)
, (5分)
化简得曲线C的直角坐标方程是 ; (6分)
; (6分)
(II)设直线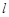 的倾斜角是
的倾斜角是 ,则
,则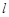 的参数方程变形为
的参数方程变形为 ,(8分)
,(8分)
代入 ,得
,得
设其两根为 ,则
,则 , (10分)
, (10分)
∴ .
.
当 时,
时, 取得最小值3. (13分)
取得最小值3. (13分)
考点:坐标系和参数方程
点评:解决的关键是对于极坐标和直角坐标的转化,以及利用参数方程求解最值,属于基础题。

练习册系列答案
相关题目
 的极坐标方程是
的极坐标方程是 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线 的参数方程为
的参数方程为 (
( 为参数).
为参数). 得到曲线
得到曲线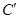 ,设
,设 为曲线
为曲线 的最小值,并求相应点
的最小值,并求相应点 的坐标。
的坐标。 和极坐标系
和极坐标系 的原点与极点重合,
的原点与极点重合, 轴正半轴与极轴重合,单位长度相同,在直角坐标系下,曲线C的参数方程为
轴正半轴与极轴重合,单位长度相同,在直角坐标系下,曲线C的参数方程为 为参数)。
为参数)。 和射线
和射线 分别交于A,B两点,求
分别交于A,B两点,求 的面积;
的面积; 的参数方程为
的参数方程为 (
( 为参数),求曲线C与直线
为参数),求曲线C与直线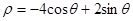 ②
②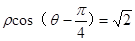
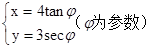 ④
④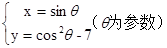
 ,在极坐标系中(与直角坐标系有相同的长度单位,极点为原点,极轴与x的非负半轴重合)曲线C:
,在极坐标系中(与直角坐标系有相同的长度单位,极点为原点,极轴与x的非负半轴重合)曲线C: ,
, ,求
,求 的值。
的值。
 ,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值.
,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值. ,圆
,圆 的参数方程为
的参数方程为 (其中
(其中 为参数).
为参数). 经过点P(1,1),倾斜角
经过点P(1,1),倾斜角
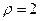 相交与A,B,求点P到A,B两点的距离积。
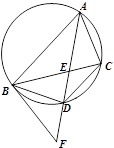
相交与A,B,求点P到A,B两点的距离积。 是圆的内接三角形,
是圆的内接三角形,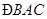 的平分线交圆于点
的平分线交圆于点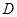 ,交
,交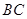 于点
于点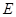 ,过点
,过点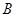 的圆的切线与
的圆的切线与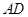 的延长线交于点
的延长线交于点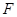 .在上述条件下,给出下列四个结论:
.在上述条件下,给出下列四个结论: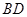 平分
平分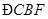 ;②
;②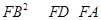 ;③
;③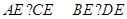 ;④
;④ .
.