题目内容
已知曲线 的极坐标方程是
的极坐标方程是 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线 的参数方程为
的参数方程为 (
( 为参数).
为参数).
(1)写出直线 的普通方程与曲线
的普通方程与曲线 的直角坐标方程;
的直角坐标方程;
(2)设曲线 经过伸缩变换
经过伸缩变换 得到曲线
得到曲线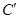 ,设
,设 为曲线
为曲线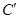 上任一点,求
上任一点,求 的最小值,并求相应点
的最小值,并求相应点 的坐标。
的坐标。
(1) ,
, ;
;
(2)当 为(
为( )或
)或 时,
时, 的最小值为1.
的最小值为1.
解析试题分析:(1)消参数方法有“加减消元法”“代入消元法”“平方关系消元法”等;将极坐标方程转化成直角坐标方程,一般利用
(2)将 代入
代入 ,即得
,即得 :
: ,应用“三角换元”思想,令
,应用“三角换元”思想,令 的坐标为:
的坐标为: ,将问题转化成三角函数值域.
,将问题转化成三角函数值域.
试题解析:(1) 2分
2分 4分
4分
(2) :
: 5分
5分
设 为:
为:
 7分
7分
所以当 为(
为( )或
)或 9分
9分 的最小值为1 10分
的最小值为1 10分
考点:参数方程与极坐标,三角函数的和差倍半公式.

练习册系列答案
相关题目
 的参数方程为
的参数方程为 ,(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为
,(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为 .
. 与圆C相切,求h.
与圆C相切,求h. 的极坐标方程为
的极坐标方程为 ,曲线
,曲线 的极坐标方程为
的极坐标方程为 ,曲线
,曲线 、
、 两点. (
两点. ( )
) (
( 为参数)分别相交于
为参数)分别相交于 两点,求线段
两点,求线段 的长度.
的长度. 的参数方程是
的参数方程是 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴,建立极坐标系,已知曲线
轴的正半轴为极轴,建立极坐标系,已知曲线 的极坐标方程为
的极坐标方程为 .
. 两点,求
两点,求 .
. 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线 的极坐标方程为
的极坐标方程为 ,过点
,过点 (-2,-4)的直线
(-2,-4)的直线 的参数方程为
的参数方程为 (
( 为参数),直线
为参数),直线 两点.
两点. ,求
,求 的值.
的值. (为参数),曲线C的极坐标方程为
(为参数),曲线C的极坐标方程为 .
. 的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线
的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线 的极坐标方程为
的极坐标方程为 .
. (
( 为参数)与曲线C交于
为参数)与曲线C交于 ,
, 两点,与
两点,与 轴交于
轴交于 ,求
,求 的值.
的值. 的极坐标是
的极坐标是 ,曲线C的极坐标方程为
,曲线C的极坐标方程为 .
. 与曲线C交于A、B两点,求
与曲线C交于A、B两点,求 的最小值.
的最小值. 的参数方程是
的参数方程是 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴,建立极坐标系,已知曲线
轴的正半轴为极轴,建立极坐标系,已知曲线 的极坐标方程为
的极坐标方程为
 .
. 的极坐标方程;
的极坐标方程; 相交于
相交于 、
、 两点,求
两点,求 .
.