题目内容
已知数列 是首项是2,公比为q的等比数列,其中
是首项是2,公比为q的等比数列,其中 是
是 与
与 的等差中项.
的等差中项.
(Ⅰ)求数列 的通项公式. (Ⅱ)求数列
的通项公式. (Ⅱ)求数列 的前n项和
的前n项和
【答案】
(1)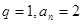
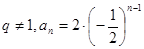
(2) 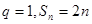
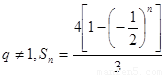
【解析】
试题分析:(Ⅰ)利用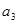 是
是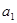 与
与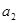 的等差中项,可求出q的值,在分类讨论即可; (Ⅱ)利用(Ⅰ)中求出的数列
的等差中项,可求出q的值,在分类讨论即可; (Ⅱ)利用(Ⅰ)中求出的数列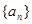 的通项公式,利用等比数列的前n项和公式即可求出
的通项公式,利用等比数列的前n项和公式即可求出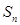 .
.
试题解析:(1)∵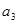 是
是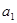 与
与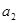 的等差中项 , ∴
的等差中项 , ∴ 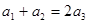 ,又数列
,又数列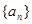 是首项是2,公比为q的等比数列,解得
是首项是2,公比为q的等比数列,解得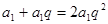 ,∴
,∴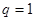 或
或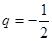 .当
.当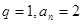 ; 当
; 当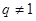 时,
时, 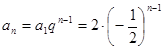 .
.
(2) 当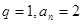 时,
时, 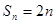 ;当
;当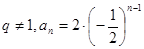 时,
时, 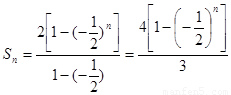 .
.
考点:1.等差中项 ; 2.等比数列的通项公式; 3.等比数列的前n项和公式

练习册系列答案
相关题目
已知数列{an}共有m项,定义{an}的所有项和为S(1),第二项及以后所有项和为S(2),第三项及以后所有项和为S(3),…,第n项及以后所有项和为S(n).若S(n)是首项为2,公比为
的等比数列的前n项和,则当n<m时,an等于( )
| 1 |
| 2 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
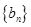 是首项为1,公差为2的等差数列,数列
是首项为1,公差为2的等差数列,数列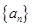 的前n项和
的前n项和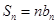 .
. , 求数列
, 求数列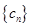 的前n项和
的前n项和 .
. 是首项为2,公差为1的等差数列,
是首项为2,公差为1的等差数列, 是首项为1,公比为2的等比数列,则数列
是首项为1,公比为2的等比数列,则数列 前10项的和等于
前10项的和等于