题目内容
(本小题共13分)设数列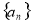 的前
的前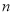 项和为
项和为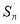 ,且
,且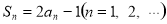 .
.
(1)求数列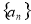 的通项公式;
的通项公式;
(2)若数列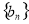 满足
满足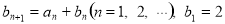 ,求数列
,求数列 的通项公式.
的通项公式.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)当 时,由
时,由 可得
可得 ,又
,又 ,所以数列
,所以数列 是等比数列,由等比数列的通项公式可求;(2)由
是等比数列,由等比数列的通项公式可求;(2)由 可得
可得 ,由累和法可数列
,由累和法可数列 的通项公式.
的通项公式.
试题解析:(1)因为 ,
,
则 ,
,
所以当 时,
时, ,
,
整理得 ,
,
由 ,令
,令 ,得
,得 ,解得
,解得 .
.
所以 是首项为1,公比为2的等比数列,可得
是首项为1,公比为2的等比数列,可得 (6分)
(6分)
(2)因为 ,
,
由 ,得
,得 ,
,
由累加得
 ,
,
当 时也满足,所以
时也满足,所以 .(13分)
.(13分)
考点:数列前 项和定义,等比数列定义及性质,累和法求数列通项.
项和定义,等比数列定义及性质,累和法求数列通项.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 :
: 与两坐标轴所围成的三角形的内切圆
与两坐标轴所围成的三角形的内切圆 的方程;
的方程;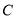 相切的直线
相切的直线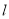 交
交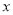 轴
轴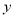 轴于
轴于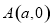 和
和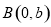 两点,且
两点,且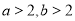 .
.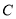 与直线
与直线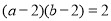 ;
;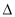 OAB面积的最小值及此时直线
OAB面积的最小值及此时直线 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
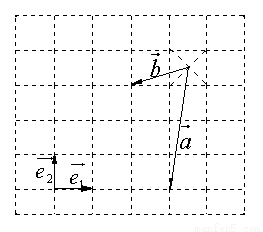
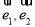 为互相垂直的两个单位向量,则
为互相垂直的两个单位向量,则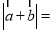 ( )
( )
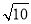 C.
C.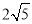 D.
D.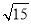
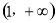 上的函数
上的函数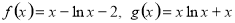
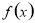 存在唯一的零点,且零点属于(3,4);
存在唯一的零点,且零点属于(3,4);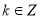 ,且
,且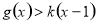 对任意的
对任意的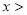 1恒成立,求
1恒成立,求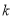 的最大值.
的最大值. ,
, ,若
,若 ,则
,则 =__________.
=__________.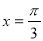 ”是“
”是“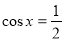 ”成立的( )
”成立的( ) 为非零常数,则“
为非零常数,则“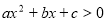 与
与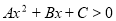 解集相同”是“
解集相同”是“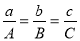 ”的
”的 是等差数列,其前n项和为Sn,若
是等差数列,其前n项和为Sn,若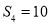 ,
,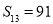 .
.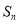 ;
; ,当
,当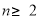 时,
时,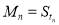 -
-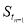 ,其中数列
,其中数列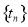 单调递增,且
单调递增,且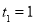 ,
,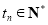 .
.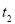 ,
,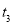 ,使得
,使得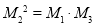 ;
;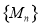 中的各数均为一个整数的平方.
中的各数均为一个整数的平方.