题目内容
(本题满分14分)
(Ⅰ)求直线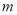 :
: 与两坐标轴所围成的三角形的内切圆
与两坐标轴所围成的三角形的内切圆 的方程;
的方程;
(Ⅱ)若与(Ⅰ)中的圆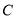 相切的直线
相切的直线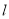 交
交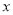 轴
轴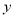 轴于
轴于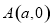 和
和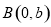 两点,且
两点,且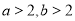 .
.
①求证:圆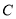 与直线
与直线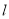 相切的条件为
相切的条件为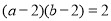 ;
;
②求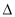 OAB面积的最小值及此时直线
OAB面积的最小值及此时直线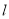 的方程.
的方程.
(Ⅰ)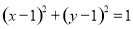 ;(Ⅱ)①见解析;②
;(Ⅱ)①见解析;② ;l:
;l:
【解析】
试题分析:【解析】
(Ⅰ)直线m:3x+4y=12与两坐标轴交点分别为A(4,0),B(0,3).
则△AOB是直角三角形
∵圆心到坐标的距离相等
∴可设圆心C(a,a),半径为a,(0<a<3)
∴圆心到AB的距离为

解得:a=1
∴圆的方程为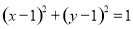 .
.
(Ⅱ)①证明:∵直线l交x轴y轴于A(a,0)和B(0,b)两点
∴直线l的方程为 ,
,
即bx+ay-ab=0
∵直线l与圆C相切,
∴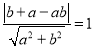
即ab-2a-2b+2=0
(a-2)(b-2)=2
②由①可知ab=2a+2b-2
∴S=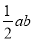 =a+b-1≥
=a+b-1≥ -1
-1
当且仅当a=b= 时取“=“
时取“=“
即S-2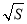 +1≥0
+1≥0
解得
∴ ,
,
∴直线l的方程为x+y-2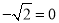
考点:本题考查直线与圆的方程的应用
点评:解决本题的关键是表示出三角形面积后,利用基本不等式和一元二次不等式的性质解决

练习册系列答案
相关题目
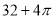 (B)
(B)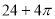 (C)
(C) (D)
(D)
 满足
满足 ,
, ,
, =2,则
=2,则 =( )
=( ) C.
C. D.2
D.2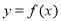 的周期为2,当
的周期为2,当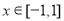 时
时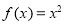 ,那么函数
,那么函数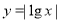 的图象的交点共有( )
的图象的交点共有( )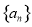 的前n项和为
的前n项和为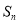 ,若
,若 ,
, ,则当
,则当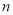 等于( )
等于( ) ,则直线
,则直线 的倾斜角的取值范围是_______________
的倾斜角的取值范围是_______________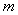 ,直线
,直线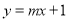 与圆
与圆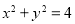 的位置关系一定是( )
的位置关系一定是( )
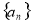 的前
的前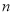 项和为
项和为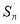 ,且
,且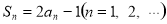 .
.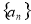 的通项公式;
的通项公式;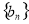 满足
满足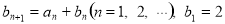 ,求数列
,求数列 的通项公式.
的通项公式.