题目内容
设A是m阶方阵,定义运算:A•A=A2,An+1=An•A(n∈N*),称这一运算为矩阵的乘方.显然矩阵的乘方满足:对任意的m,n∈N*,Am•An=Am+n,设A=
|
分析:利用矩阵乘法的定义有A2=A•A =
=
=
,再利用An+1=An•A可求.
|
|
|
|
解答:解:A2=A•A =
=
=
,A3=A2•A=
=
,同理A4=
,猜想 An=
,
故答案为:An=
|
|
|
|
|
|
|
|
|
故答案为:An=
|
点评:本题主要考查矩阵乘法,矩阵的乘方,利用好定义、性质是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 ,计算A2,A3,A4,并对一切正整数n,猜想An= .
,计算A2,A3,A4,并对一切正整数n,猜想An= .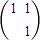 ,则A3= .
,则A3= .