题目内容
已知椭圆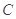 过点
过点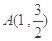 ,两个焦点为
,两个焦点为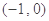 ,
,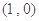 .
.
(1)求椭圆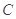 的方程;
的方程;
(2)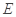 ,
,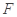 是椭圆
是椭圆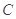 上的两个动点,如果直线
上的两个动点,如果直线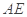 的斜率与
的斜率与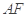 的斜率互为相反数,证明直线
的斜率互为相反数,证明直线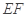 的斜率为定值,并求出这个定值.
的斜率为定值,并求出这个定值.
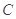 过点
过点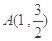 ,两个焦点为
,两个焦点为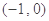 ,
,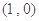 .
.(1)求椭圆
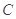 的方程;
的方程;(2)
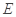 ,
,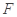 是椭圆
是椭圆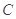 上的两个动点,如果直线
上的两个动点,如果直线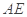 的斜率与
的斜率与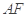 的斜率互为相反数,证明直线
的斜率互为相反数,证明直线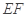 的斜率为定值,并求出这个定值.
的斜率为定值,并求出这个定值.(1) 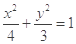 (2)直线
(2)直线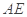 的斜率为定值
的斜率为定值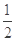
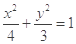 (2)直线
(2)直线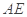 的斜率为定值
的斜率为定值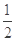
试题分析:(1) 由题意
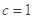 ,设椭圆方程为
,设椭圆方程为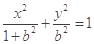 ,将
,将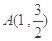 代入即可求出
代入即可求出 ,则椭圆方程可求.
,则椭圆方程可求.(2)设直线AE方程为:
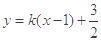 ,代入入
,代入入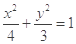 得
得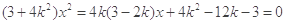 ,再由点
,再由点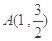 在椭圆上,根据结直线
在椭圆上,根据结直线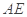 的斜率与
的斜率与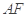 的斜率互为相反数,结合直线的位置关系进行求解.
的斜率互为相反数,结合直线的位置关系进行求解.(1)由题意
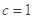 ,设椭圆方程为
,设椭圆方程为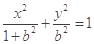 ,
,因为点
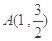 在椭圆上,所以
在椭圆上,所以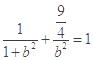 ,解得
,解得 ,
,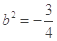
所求椭圆方程为
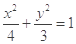
(2)设直线
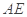 方程为
方程为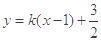 ,代入
,代入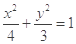 得
得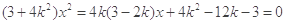
设
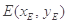 ,
,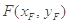 ,点
,点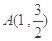 在直线
在直线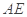 上
上则
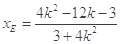 ,
,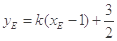 ;
;直线
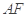 的斜率与直线
的斜率与直线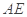 的斜率互为相反数,在上式中用
的斜率互为相反数,在上式中用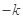 代替
代替 得
得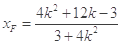 ,
,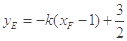 ,
,直线
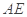 的斜率
的斜率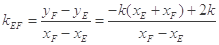
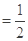
所以直线
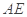 的斜率为定值
的斜率为定值
练习册系列答案
相关题目
 +
+ =1(a>b>0)的左、右焦点,点P(-
=1(a>b>0)的左、右焦点,点P(- ,1)在椭圆上,线段PF2与y轴的交点M满足
,1)在椭圆上,线段PF2与y轴的交点M满足 +
+ =0.
=0. +
+ =1(m<6)与曲线
=1(m<6)与曲线 +
+ =1(5<n<9)的( )
=1(5<n<9)的( ) 过点
过点 且离心率为
且离心率为 .
. 的方程;
的方程; 的直线
的直线 交
交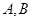 两点,且
两点,且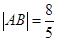 ,求直线
,求直线
 或2
或2 2
2
 ,
, 的坐标分别为
的坐标分别为 ,
, .直线
.直线 ,
, 相交于点
相交于点 ,且它们的斜率之积是
,且它们的斜率之积是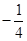 ,记动点
,记动点 .
.  是曲线
是曲线 ,
, 分别交直线
分别交直线 于点
于点 ,线段
,线段 的中点为
的中点为 ,求直线
,求直线 与直线
与直线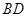 的斜率之积的取值范围;
的斜率之积的取值范围; 与
与 的交点为
的交点为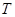 ,试探究点
,试探究点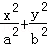 =1(a>b>0)与双曲线C2:x2﹣
=1(a>b>0)与双曲线C2:x2﹣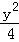 =1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
=1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )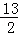

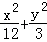 =1的焦点为F1和F2,点P在椭圆上,如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的( )
=1的焦点为F1和F2,点P在椭圆上,如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的( ) 表示椭圆,则实数
表示椭圆,则实数 的取值范围为
的取值范围为