题目内容
下列说法正确的是 .
①y=sinx+
(0<x≤
)的最小值为4
②y=
的最小值为2
③y=ex+e-x的最小值为2
④x>0,y>0,且x+y=20,则m=lgx+lgy的最大值为2.
①y=sinx+
| 4 |
| sinx |
| π |
| 2 |
②y=
| x2+5 | ||
|
③y=ex+e-x的最小值为2
④x>0,y>0,且x+y=20,则m=lgx+lgy的最大值为2.
考点:命题的真假判断与应用
专题:不等式的解法及应用
分析:①令sinx=t(0<t≤1),则y=t+
,求导数,判断单调性,再求最值,注意运用基本不等式,等号不成立;
②令
=t(t≥2),则y=t+
,若运用基本不等式求最值,等号不成立,可用导数判断单调性,从而求出最值;
③运用基本不等式求出最值,注意等号成立的条件;
④运用基本不等式求最值,注意运用对数的运算法则和变形:xy≤(
)2即可.
| 4 |
| t |
②令
| x2+4 |
| 1 |
| t |
③运用基本不等式求出最值,注意等号成立的条件;
④运用基本不等式求最值,注意运用对数的运算法则和变形:xy≤(
| x+y |
| 2 |
解答:
解:①y=sinx+
(0<x≤
),令sinx=t(0<t≤1),则y=t+
,由于y′=1-
<0,故(0,1]为减区间,故最小值为5,故①错;
②y=
,令
=t(t≥2),则y=t+
≥2,t=1时取最小值,但t≥2,故最小值不为2,由于y′=1-
>0,故[2,+∞)为增区间,故最小值为
,即②错;
③由于ex>0,e-x>0,则y=ex+e-x≥2,当且仅当x=0,y取最小值2,故③正确;
④x>0,y>0,且x+y=20,则m=lgx+lgy=lg(xy)≤lg(
)2=lg100=2,当且仅当x=y=10,m取最大值2,故④正确.
故答案为:③④.
| 4 |
| sinx |
| π |
| 2 |
| 4 |
| t |
| 4 |
| t2 |
②y=
| x2+5 | ||
|
| x2+4 |
| 1 |
| t |
| 1 |
| t2 |
| 5 |
| 2 |
③由于ex>0,e-x>0,则y=ex+e-x≥2,当且仅当x=0,y取最小值2,故③正确;
④x>0,y>0,且x+y=20,则m=lgx+lgy=lg(xy)≤lg(
| x+y |
| 2 |
故答案为:③④.
点评:本题以命题的真假为载体,考查基本不等式的运用,主要是求最值,应注意等号成立的条件,同时考查运用导数判断单调性,求最值.

练习册系列答案
相关题目
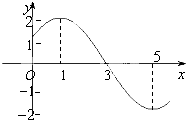 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<