题目内容
已知O为坐标原点，向量
=（sinα，1），
=（cosα，0），
=（-sinα，2），点P满足
=
（1）记f（α）=
•
，α∈（-
，
），求函数f（α）的值域；
（2）若O，P，C三点共线，求|
+
|的值．
| OA |
| OB |
| OC |
| AB |
| BP |
（1）记f（α）=
| BP |
| CA |
| π |
| 8 |
| π |
| 2 |
（2）若O，P，C三点共线，求|
| OA |
| OB |
分析：（1）设出P的坐标，由向量的坐标得到点的坐标，再由点的坐标求出所用向量的坐标，结合
=
求出P的坐标，代入f（α）=
•
化简，由α的范围可求函数f（α）的值域；
（2）由O，P，C三点共线，由向量共线的充要条件求出tanα的值，结合|
+
|=
，利用万能公式，代入即可求出|
+
|的值．
| AB |
| BP |
| BP |
| CA |
（2）由O，P，C三点共线，由向量共线的充要条件求出tanα的值，结合|
| OA |
| OB |
| sin2α+2 |
| OA |
| OB |
解答：解：（1）设点P的坐标为（x，y），
∵
=（sinα，1），
=（cosα，0），
=（-sinα，2），
∴A（sinα，1），B（cosα，0），C（-sinα，2），
∴
=（cosα-sinα，-1），
=（x-cosα，y），
由
=
，得cosα-sinα=x-cosα，y=-1．
∴x=2cosα-sinα，y=-1，
∴点P的坐标为（2cosα-sinα，-1），
∴
=(cosα-sinα，-1)，
=(2sinα，-1)．
则f（α）=
•
=2sinαcosα-2sin2α+1
=sin2α+cos2α
=
sin(2α+
)．
∵α∈（-
，
），∴2α+
∈(0，
)，
∴f（α）∈（-1，
]；
（2）∵O，P，C三点共线，
∴-1×（-sinα）=2×（2cosα-sinα），
∴tanα=
，
∴sin2α=
=
，
∴|
+
|=
=
=
．
∵
| OA |
| OB |
| OC |
∴A（sinα，1），B（cosα，0），C（-sinα，2），
∴
| AB |
| BP |
由
| AB |
| BP |
∴x=2cosα-sinα，y=-1，
∴点P的坐标为（2cosα-sinα，-1），
∴
| BP |
| CA |
则f（α）=
| BP |
| CA |
=2sinαcosα-2sin2α+1
=sin2α+cos2α
=
| 2 |
| π |
| 4 |
∵α∈（-
| π |
| 8 |
| π |
| 2 |
| π |
| 4 |
| 5π |
| 4 |
∴f（α）∈（-1，
| 2 |
（2）∵O，P，C三点共线，
∴-1×（-sinα）=2×（2cosα-sinα），
∴tanα=
| 4 |
| 3 |
∴sin2α=
| 2tanα |
| 1+tan2α |
| 24 |
| 25 |
∴|
| OA |
| OB |
| (sinα+cosα)2+1 |
| sin2α+2 |
| ||
| 5 |
点评：本题考查的知识点是平面向量数量积的坐标表示，正弦型函数的单调性，两角和与差的正弦，二倍角的正弦，二倍角的余弦，三点共线，解题的关键是根据向量共线的充要条件求出tanα的值，是中档题．
练习册系列答案
相关题目
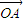=（sinα，1），
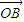=（cosα，0），
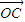=（-sinα，2），点P是直线AB上的一点，且点B分有向线段
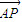的比为1．
•
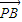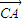，α∈（-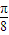
，
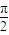），讨论函数f（α）的单调性，并求其值域；
+
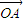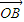|的值．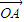
=（sinα，1），
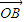=（cosα，0），
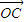=（-sinα，2），点P是直线AB上的一点，且点B分有向线段
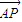的比为1．
•
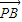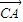，α∈（-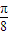
，
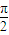），讨论函数f（α）的单调性，并求其值域；
+
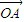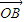|的值．