题目内容
5.指数函数y=($\frac{b}{a}$)x的图象如图所示,则二次函数y=ax2+bx的顶点的横坐标的取值范围是(-$\frac{1}{2}$,0).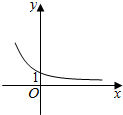
分析 根据指数函数的图象求出$\frac{b}{a}$的取值范围,利用二次函数的性质进行求解即可.
解答 解:由图象知函数为减函数,则0<$\frac{b}{a}$<1,
二次函数y=ax2+bx的顶点的横坐标为x=-$\frac{b}{2a}$,
∵0<$\frac{b}{a}$<1,
∴0<$\frac{b}{2a}$<$\frac{1}{2}$,-$\frac{1}{2}$<-$\frac{b}{2a}$<0,
即横坐标的取值范围是(-$\frac{1}{2}$,0),
故答案为:(-$\frac{1}{2}$,0).
点评 本题主要考查指数函数和二次函数的性质,根据条件求出$\frac{b}{a}$的取值范围是解决本题的关键.

练习册系列答案
相关题目
20.若A(-2,3),B(3,-2),C(0,m)三点共线,则m的值为( )
| A. | 1 | B. | -1 | C. | -5 | D. | 5 |
10.某企业上半年产品产量与单位成本资料如表:
且已知产量x与成本y具有线性相关关系(a,b用小数表示,结果精确到0.01).
(1)求出y关于x的线性回归方程(给出数据$\sum_{i=1}^{n}$xiyi=1481);
(2)指出产量每增加1000件时,单位成本平均变动多少?
(3)假定产量为6000件时,单位成本为多少元?
| 月份 | 产量(千件) | 单位成本(元) |
| 1 | 2 | 73 |
| 2 | 3 | 72 |
| 3 | 4 | 71 |
| 4 | 3 | 73 |
| 5 | 4 | 69 |
| 6 | 5 | 68 |
(1)求出y关于x的线性回归方程(给出数据$\sum_{i=1}^{n}$xiyi=1481);
(2)指出产量每增加1000件时,单位成本平均变动多少?
(3)假定产量为6000件时,单位成本为多少元?
14.如果甲、乙在围棋比赛中,甲不输的概率为60%,甲获胜的概率为50%,则甲、乙和棋的概率为( )
| A. | 50% | B. | 40% | C. | 20% | D. | 10% |