题目内容
“当一个圆与一个正方形的周长相等时，这个圆的面积比正方形的面积大”，将此结论由平面类比到空间的一个正确的命题：
当一个球与一个正方体的表面积相等时，这个球的体积比正方形的体积大
当一个球与一个正方体的表面积相等时，这个球的体积比正方形的体积大
．分析：在由平面几何的性质类比推理空间立体几何性质时，我们常用的思路是：由平面几何中点的性质，类比推理空间几何中线的性质；由平面几何中线的性质，类比推理空间几何中面的性质；由平面几何中面的性质，类比推理空间几何中体的性质；故由：当一个圆与一个正方形的周长相等时，这个圆的面积比正方形的面积大，类比到空间可得的结论是：当一个球与一个正方体的表面积相等时，这个球的体积比正方形的体积大．
解答：解：在由平面几何的性质类比推理空间立体几何性质时，
一般为：由平面几何中点的性质，类比推理空间几何中线的性质；
由平面几何中线的性质，类比推理空间几何中面的性质；
由平面几何中面的性质，类比推理空间几何中体的性质；
故由：“当一个圆与一个正方形的周长相等时，这个圆的面积比正方形的面积大”，
类比到空间可得的结论是：
当一个球与一个正方体的表面积相等时，这个球的体积比正方形的体积大
故答案为：当一个球与一个正方体的表面积相等时，这个球的体积比正方形的体积大．
一般为：由平面几何中点的性质，类比推理空间几何中线的性质；
由平面几何中线的性质，类比推理空间几何中面的性质；
由平面几何中面的性质，类比推理空间几何中体的性质；
故由：“当一个圆与一个正方形的周长相等时，这个圆的面积比正方形的面积大”，
类比到空间可得的结论是：
当一个球与一个正方体的表面积相等时，这个球的体积比正方形的体积大
故答案为：当一个球与一个正方体的表面积相等时，这个球的体积比正方形的体积大．
点评：本题考查的知识点是类比推理，类比推理的一般步骤是：（1）找出两类事物之间的相似性或一致性；（2）用一类事物的性质去推测另一类事物的性质，得出一个明确的命题（猜想）．
练习册系列答案
综合自测系列答案
相关题目
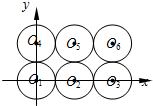如图，有6个半径都为1的圆，其圆心分别为O1（0，0），O2（2，0），O3（4，0），O4（0，2），O5（2，2），O6（4，2）．记集合M={⊙Oi|i=1，2，3，4，5，6}．若A，B为M的非空子集，且A中的任何一个圆与B中的任何一个圆均无公共点，则称 （A，B） 为一个“有序集合对”（当A≠B时，（A，B） 和 （B，A） 为不同的有序集合对），那么M中“有序集合对”（A，B） 的个数是（ ）