题目内容
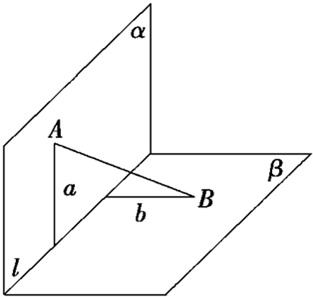 如图,α⊥β,α∩β=l,A∈α,B∈β,A、B到l的距离分别是a和b,AB与α、β所成的角分别是θ和φ,AB在α、β内的射影分别是m和n.若a>b,则θ与φ的大小关系为________,m与n的大小关系为________.
如图,α⊥β,α∩β=l,A∈α,B∈β,A、B到l的距离分别是a和b,AB与α、β所成的角分别是θ和φ,AB在α、β内的射影分别是m和n.若a>b,则θ与φ的大小关系为________,m与n的大小关系为________.
θ<φ m>n
分析:画出图形,AB与β成的角为∠ABC=φ,AB与α成的角为∠BAD=θ,通过三角计算,说明sinφ>sinθ推出θ<φ.利用射影关系说明m>n.
解答: 解:AB与β成的角为∠ABC=φ,
解:AB与β成的角为∠ABC=φ,
AB与α成的角为∠BAD=θ,
sinφ=sin∠ABC= ,
,
sinθ=sin∠BAD= .
.
∵a>b,∴sinφ>sinθ.∴θ<φ.
AB在α内的射影AD= ,
,
AB在β内的射影BC= ,
,
∴AD.BC,即m>n.
故答案为:θ<φ;m>n
点评:本题是中档题,考查直线与平面的位置关系,直线在平面内的射影,三角计算,大小比较,考查计算能力,逻辑推理能力.
分析:画出图形,AB与β成的角为∠ABC=φ,AB与α成的角为∠BAD=θ,通过三角计算,说明sinφ>sinθ推出θ<φ.利用射影关系说明m>n.
解答:
 解:AB与β成的角为∠ABC=φ,
解:AB与β成的角为∠ABC=φ,AB与α成的角为∠BAD=θ,
sinφ=sin∠ABC=
 ,
,sinθ=sin∠BAD=
 .
.∵a>b,∴sinφ>sinθ.∴θ<φ.
AB在α内的射影AD=
 ,
,AB在β内的射影BC=
 ,
,∴AD.BC,即m>n.
故答案为:θ<φ;m>n
点评:本题是中档题,考查直线与平面的位置关系,直线在平面内的射影,三角计算,大小比较,考查计算能力,逻辑推理能力.

练习册系列答案
相关题目
 9、如图所示的程序框图的输出结果为( )
9、如图所示的程序框图的输出结果为( )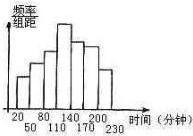
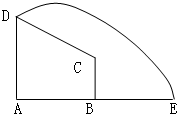 如图,在直角梯形ABCD中,AD∥BC,DA⊥AB,AD=3,AB=4,
如图,在直角梯形ABCD中,AD∥BC,DA⊥AB,AD=3,AB=4, 5、执行如图所示的程序框图,输出的T=
5、执行如图所示的程序框图,输出的T=