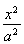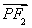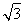Question

在如图所示的几何体中，四边形ABCD是菱形，ADNM是矩形，平面ADNM⊥平面ABCD，P为DN的中点．

(1)求证：BD⊥MC；

(2)线段AB上是否存在点E，使得AP∥平面NEC？若存在，说明在什么位置，并加以证明；若不存在，说明理由．

 

Answer 1

（1）见解析（2）E为AB的中点时，有AP∥平面NEC

【解析】(1)证明：联结AC，因为四边形ABCD是菱形，

所以AC⊥BD.

又四边形ADNM是矩形，平面ADNM⊥平面ABCD，平面ADNM∩平面ABCD＝AD，AM⊥AD，所以AM⊥平面ABCD.

因为BD平面ABCD，所以AM⊥BD.

因为AC∩AM＝A，所以BD⊥平面MAC.

又MC平面MAC，所以BD⊥MC.

(2)当E为AB的中点时，有AP∥平面NEC.

取NC的中点S，联结PS，SE.

因为PS∥DC∥AE，PS＝AE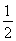＝DC，

所以四边形APSE是平行四边形，所以AP∥SE.

又SE?平面NEC，AP?平面NEC，所以AP∥平面NEC.