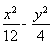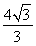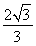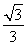题目内容
设F1，F2为双曲线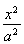
－y2＝1的两个焦点，已知点P在此双曲线上，且
·
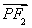＝0.若此双曲线的离心率等于
，则点P到x轴的距离等于________．
【解析】∵
－y2＝1的离心率等于
，∴
＝
，∴a2＝4.
∵点P在双曲线
－y2＝1上，∴(|PF1|－|PF2|)2＝16，
即|PF1|2＋|PF2|2－2|PF1||PF2|＝16.又∵
·
＝0，∴PF⊥PF2，
∴|F1F2|2－2|PF1||PF2|＝16，解得|PF1||PF2|＝2.
设P点到x轴的距离等于d，则
|F1F2|·d＝
|PF1||PF2|.解得d＝
练习册系列答案
相关题目
