题目内容
【题目】在平面直角坐标系中，△ABC三个顶点分别为A（2，4），B（1，﹣3），C（﹣2，1）．
（1）求BC边上的高所在的直线方程；
（2）设AC中点为D，求△DBC的面积．
【答案】
（1）解：kBC= 
=﹣ 
，∴BC边上的高所在的直线的斜率为 
．
则BC边上的高所在的直线方程为：y﹣4= （x﹣2），化为：3x﹣4y+10=0．
（2）解：BC边所在的直线方程为：y+3=﹣ （x﹣1），化为：4x+3y+5=0．
∵D是AC的中点，∴D 
．
点D到直线BC的距离d=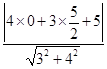 
= 
．
又|BC|= 
=5，
∴S△DBC= 
= 
= 
．
【解析】（1）kBC=﹣ 
，可得BC边上的高所在的直线的斜率为 
．利用点斜式可得BC边上的高所在的直线方程．（2）BC边所在的直线方程为：y+3=﹣ （x﹣1），化为：4x+3y+5=0．可得AC的中点D 
．利用点D到直线BC的距离d．又|BC|，可得S△DBC= 
．
【考点精析】解答此题的关键在于理解点到直线的距离公式的相关知识，掌握点
到直线
的距离为：
．
练习册系列答案
相关题目
