Question

【题目】如图，在直三棱柱ABC﹣A1B1C1中，∠ACB=90°，AA1=2，AC=BC=1，则异面直线A1B与AC所成角的余弦值是（ ）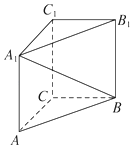
A.
B.
C.
D.

Answer 1

【答案】D
【解析】解：连结BC1 ， ∵AC∥A1C1 ， ∴∠C1A1B是异面直线A1B与AC所成角（或所成角的补角），
∵在直三棱柱ABC﹣A1B1C1中，∠ACB=90°，AA1=2，AC=BC=1，
∴AB= ， ，BC1= = ，A1C1=1，
∴cos∠C1A1B= = = ，
∴异面直线A1B与AC所成角的余弦值为 ．
故选：D．

由AC∥A1C1 ， 知∠C1A1B是异面直线A1B与AC所成角（或所成角的补角），由此能求出异面直线A1B与AC所成角的余弦值．