题目内容
【题目】已知点F(2,0),动点P满足:点P到直线x=-1的距离比其到点F的距离小1.
(Ⅰ)求点P的轨迹C的方程;
(Ⅱ)过F作直线l垂直于x轴与曲线C交于A、B两点,Q是曲线C上异于A、B的一点,设曲线C在点A、B、Q处的切线分别为l1、l2、l3,切线l1、l2交于点R,切线l1、l3交于点S,切线l2、l3交于点T,若![]() RST的面积为6,求Q点的横坐标.
RST的面积为6,求Q点的横坐标.
【答案】(Ⅰ)直线![]() 的普通方程为
的普通方程为![]() ,轨迹C的方程为
,轨迹C的方程为![]() ;(Ⅱ)
;(Ⅱ)![]() 点的横坐标为
点的横坐标为![]() .
.
【解析】
(1)利用抛物线的定义求出![]() 的方程.
的方程.
(2)求出![]() 两点的坐标后求出曲线
两点的坐标后求出曲线![]() 在
在![]() 三点处的切线方程,求出交点
三点处的切线方程,求出交点![]() 的坐标后可计算
的坐标后可计算![]() 面积,从而得到
面积,从而得到![]() 的坐标.
的坐标.
(1)点![]() 到
到![]() 的距离与点
的距离与点![]() 到直线
到直线![]() 的距离相等,故
的距离相等,故![]() 的轨迹为抛物线,从而
的轨迹为抛物线,从而![]() .
.
(2)令![]() ,则
,则![]() ,
, ![]() .
.
当![]() 时,有
时,有![]() ,故抛物线在
,故抛物线在![]() 处切线的斜率为
处切线的斜率为![]() ,故在
,故在![]() 处切线方程为
处切线方程为![]() .
.
同理![]() 处切线方程为
处切线方程为![]() .故
.故![]() .
.
若![]() ,则
,则![]() ,舎;
,舎;
若![]() ,可设
,可设![]() 在第一象限,则抛物线在
在第一象限,则抛物线在![]() 处切线的斜率为
处切线的斜率为![]() ,故在
,故在![]() 处切线方程为
处切线方程为![]() .
.
由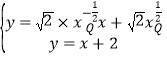 得
得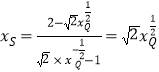 ,
,
同理![]() ,所以
,所以![]() ,
,![]()
![]() ,解得
,解得![]() 或
或![]() (舎).
(舎).

【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(Ⅰ)根据表中数据,建立![]() 关于的线性回归方程
关于的线性回归方程![]() ;
;
(Ⅱ)根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留小数点后两位)
,计算结果保留小数点后两位)
【题目】2019年1月1日起我国实施了个人所得税的新政策,新政策的主要内容有:①个税起征点为5000元,②每月应纳税所得额(含税)=收入![]() 个税起征点
个税起征点![]() 专项附加扣除.赵先生某月收入
专项附加扣除.赵先生某月收入![]() 元,符合赡养老人与子女教育专项附加扣除,共计3000元.
元,符合赡养老人与子女教育专项附加扣除,共计3000元.
新个税政策的税率表部分内容如下:
级数 | 一级 | 二级 | 三级 | … |
每月应纳税所得额(含税) | 不超过3000元的部分 | 超过3000元至12000元的部分 | 超过12000元25000元的部分 | … |
税率(%) | 3 | 10 | 20 | … |
(1)当![]() 时,赵先生当月应缴纳的个税额是多少?
时,赵先生当月应缴纳的个税额是多少?
(2)设赵先生当月应缴纳的个税额是![]() 元,若
元,若![]() ,请求出
,请求出![]() 关于
关于![]() 的函数;
的函数;
(3)若赵先生该月应纳的个税额为3020元,问他的月收入![]() 是多少元?
是多少元?
