Question

已知矩形ABCD中，AB=2，AD=5，E，F分别在AD，BC上且AE=1，BF=3，将四边形AEFB沿EF折起，使点B在平面CDEF上的射影H在直线DE上．

       

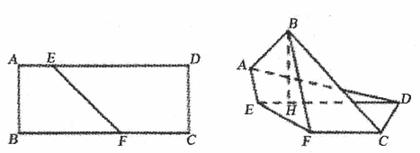
    （1）求证：AD//平面BFC；

    （2）求二面角A- DE -F的平面角的大小．

Answer 1

解：（1）∵AE//BF，DE//FC

        ∴AE∥平面BFC，∥平面BFC          

∴平面∥平面BFC      

∴AD∥平面BFC

（2）方法一：      

由（I）可知平面∥平面BFC

 ∴二面角与二面角互补

过作于，连结

        ∵平面   ∴  ∴平面  ∴

        ∵，

∴  ∵ ∴

        又∵，   ∴  

∵   ∴…………8分

过作交延长线于点，连结

∵平面   ∴   

∴平面     ∴

∴为二面角的平面角   

∵   ∴

∴二面角的大小为…

        方法二：     

 如图，过作∥，过作平面

        分别以，，为，，轴建立空间直角坐标系

        ∵在平面上的射影在直线上，设

        ∵，，

        ∴  

∴

       ∴         

       ∴

       设平面的法向量为  又有

         

又∵平面的法向量为

       设二面角的大小为，显然为钝角

∴   ∴