题目内容
已知向量a=(sinx,cosx),b=(cosx,cosx),f(x)=a•(a+b).
(1)求函数f(x)的最小正周期;
(2)当 时,求函数f(x)的值域.
时,求函数f(x)的值域.
解:(1) =(sinx+cosx,2cosx)
=(sinx+cosx,2cosx)
f(x)= =sin2x+sinxcosx+2cos2x=
=sin2x+sinxcosx+2cos2x= +
+ sin2x+
sin2x+ cos2x=
cos2x= sin(2x+
sin(2x+ )
)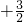
∴f(x)的最小正周期是π
(2)由(1)知,f(x)= sin(2x+
sin(2x+ )
)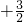
由 得
得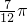 ≤2x+
≤2x+ ≤
≤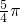 ,
,
∴- ≤sin(2x+
≤sin(2x+ )≤
)≤
∴f(x)的最大值是 ,最小值是1.
,最小值是1.
分析:(1)利用函数f(x)= ,通过二倍角公式、两角和的正弦函数化简函数为一个角的一个三角函数的形式,然后求出周期.
,通过二倍角公式、两角和的正弦函数化简函数为一个角的一个三角函数的形式,然后求出周期.
(2)由 求出
求出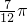 ≤2x+
≤2x+ ≤
≤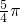 ,结合正弦函数的最值,求出函数f(x)在区间上的最大值和最小值.
,结合正弦函数的最值,求出函数f(x)在区间上的最大值和最小值.
点评:本题是基础题,考查三角函数的化简求值,向量的数量积的应用,三角函数的闭区间上的最值的求法,考查计算能力.
 =(sinx+cosx,2cosx)
=(sinx+cosx,2cosx)f(x)=
 =sin2x+sinxcosx+2cos2x=
=sin2x+sinxcosx+2cos2x= +
+ sin2x+
sin2x+ cos2x=
cos2x= sin(2x+
sin(2x+ )
)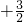
∴f(x)的最小正周期是π
(2)由(1)知,f(x)=
 sin(2x+
sin(2x+ )
)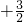
由
 得
得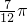 ≤2x+
≤2x+ ≤
≤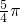 ,
,∴-
 ≤sin(2x+
≤sin(2x+ )≤
)≤
∴f(x)的最大值是
 ,最小值是1.
,最小值是1.分析:(1)利用函数f(x)=
 ,通过二倍角公式、两角和的正弦函数化简函数为一个角的一个三角函数的形式,然后求出周期.
,通过二倍角公式、两角和的正弦函数化简函数为一个角的一个三角函数的形式,然后求出周期.(2)由
 求出
求出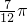 ≤2x+
≤2x+ ≤
≤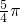 ,结合正弦函数的最值,求出函数f(x)在区间上的最大值和最小值.
,结合正弦函数的最值,求出函数f(x)在区间上的最大值和最小值.点评:本题是基础题,考查三角函数的化简求值,向量的数量积的应用,三角函数的闭区间上的最值的求法,考查计算能力.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目