题目内容
椭圆的两焦点把椭圆的对称轴上夹在两准线间的线段三等分,则椭圆的离心率为 .
【答案】分析:确定椭圆的两准线间的距离、两焦点间的距离,利用两焦点三等分椭圆两准线间的距离,建立方程,即可求得椭圆的离心率.
解答:解:两准线间的距离为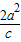 ,两焦点间的距离2c,
,两焦点间的距离2c,
∵两焦点三等分椭圆两准线间的距离,
∴2c= •
•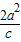 ,即:6c2=2a2,
,即:6c2=2a2,
∴e=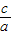 =
=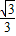
故答案为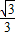 .
.
点评:本题考查椭圆的性质,考查学生的计算能力,属于基础题.
解答:解:两准线间的距离为
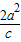 ,两焦点间的距离2c,
,两焦点间的距离2c,∵两焦点三等分椭圆两准线间的距离,
∴2c=
 •
•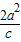 ,即:6c2=2a2,
,即:6c2=2a2,∴e=
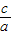 =
=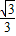
故答案为
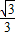 .
.点评:本题考查椭圆的性质,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
 (2013•浦东新区二模)(1)设椭圆C1:
(2013•浦东新区二模)(1)设椭圆C1: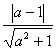
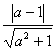
 的两个焦点为F1,F2,则这个椭圆上存在六个不同的点M,使得△F1MF2为直角三角形;
的两个焦点为F1,F2,则这个椭圆上存在六个不同的点M,使得△F1MF2为直角三角形; 的一个焦点作它的一条渐近线的垂线,垂足为M,O为坐标原点,则|OM|=a;
的一个焦点作它的一条渐近线的垂线,垂足为M,O为坐标原点,则|OM|=a;