题目内容
 如图所示的多面体V-ABCD,它的正视图为直角三角形,侧视图为等腰三角形,俯视图的边界为正方形(尺寸如图所示,单位:cm).
如图所示的多面体V-ABCD,它的正视图为直角三角形,侧视图为等腰三角形,俯视图的边界为正方形(尺寸如图所示,单位:cm).(I)求多面体V-ABCD的表面积;
(II)设
| VE |
| VB |
分析:(I)多面体V-ABCD的表面积为S△VAB+S正方形ABCD+S△VAD+S△VCD,即可得到结论;
(II)设AB,CD的中点为O,F,连接VO,OF,则OB,OF,OV两两垂直,以O为原点,OB,OF,OV所在直线为x,y,z轴,建立空间直角坐标系,确定平面VCD与平面EAC的法向量,利用平面VCD与平面EAC所成的锐角为30°,即可求得结论.
(II)设AB,CD的中点为O,F,连接VO,OF,则OB,OF,OV两两垂直,以O为原点,OB,OF,OV所在直线为x,y,z轴,建立空间直角坐标系,确定平面VCD与平面EAC的法向量,利用平面VCD与平面EAC所成的锐角为30°,即可求得结论.
解答:解:(I)由题意,S△VAB=
×2×2=2,S正方形ABCD=2×2=4
在△VBC中,BC=2,VB=
,且VB⊥BC,∴S△VBC=
×2×
=
同理可得S△VAD=
×2×
=
在△VCD中,VC=VD=3,CD=2,∴S△VCD=
×2×2
=2
∴多面体V-ABCD的表面积为6+2
+2
;
(II)设AB,CD的中点为O,F,连接VO,OF,则OB,OF,OV两两垂直,以O为原点,OB,OF,OV所在直线为x,y,z轴,建立空间直角坐标系
则A(-1,0,0),B(1,0,0),C(1,2,0),D(-1,2,0),V(0,0,2),E(
,0,1)
设平面VCD的一个法向量为
=(x,y,z)
∵
=(-1,-2,2),
=(-2,0,0)
∴由
可得
,∴可取
=(0,1,1)
设平面EAC的一个法向量为
=(x′,y′,z′)
∵
=λ
=(λ,0,-2λ),
=(-1,0,-2)
∴
=
-
=(-1-λ,0,2λ-2)
∵
=(2,2,0)
∴
,∴可取
=(2λ-2,-2λ+2,λ+1)
∵平面VCD与平面EAC所成的锐角为30°
∴cos<
,
>=
=
∴25λ2-30λ+9=0
∴λ=
∴存在λ=
,使得平面VCD与平面EAC所成的锐角为30°
| 1 |
| 2 |
在△VBC中,BC=2,VB=
| 5 |
| 1 |
| 2 |
| 5 |
| 5 |
同理可得S△VAD=
| 1 |
| 2 |
| 5 |
| 5 |
在△VCD中,VC=VD=3,CD=2,∴S△VCD=
| 1 |
| 2 |
| 2 |
| 2 |
∴多面体V-ABCD的表面积为6+2
| 5 |
| 2 |
(II)设AB,CD的中点为O,F,连接VO,OF,则OB,OF,OV两两垂直,以O为原点,OB,OF,OV所在直线为x,y,z轴,建立空间直角坐标系

则A(-1,0,0),B(1,0,0),C(1,2,0),D(-1,2,0),V(0,0,2),E(
| 1 |
| 2 |
设平面VCD的一个法向量为
| n |
∵
| VC |
| CD |
∴由
|
|
| n |
设平面EAC的一个法向量为
| m |
∵
| VE |
| VB |
| VA |
∴
| EA |
| VA |
| VE |
∵
| AC |
∴
|
| m |
∵平面VCD与平面EAC所成的锐角为30°
∴cos<
| m |
| n |
| |-λ+3| | ||||
|
| ||
| 2 |
∴25λ2-30λ+9=0
∴λ=
| 3 |
| 5 |
∴存在λ=
| 3 |
| 5 |
点评:本题考查多面体的表面积,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 (2013•宁德模拟)如图所示的多面体A1ADD1BCC1中,底面ABCD为正方形,AA1∥BB1∥CC1,AA12AB=2AA1=CC1=DD1=4,且AA1⊥底面ABCD.
(2013•宁德模拟)如图所示的多面体A1ADD1BCC1中,底面ABCD为正方形,AA1∥BB1∥CC1,AA12AB=2AA1=CC1=DD1=4,且AA1⊥底面ABCD.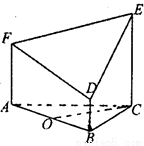
 如图所示的多面体V-ABCD,它的正视图为直角三角形,侧视图为等腰三角形,俯视图的边界为正方形(尺寸如图所示,单位:cm).
如图所示的多面体V-ABCD,它的正视图为直角三角形,侧视图为等腰三角形,俯视图的边界为正方形(尺寸如图所示,单位:cm). ,是否存在实数λ使得平面VCD与平面EAC所成的锐角为30°?若存在,求出实数λ的值;若不存在,请说明理由.
,是否存在实数λ使得平面VCD与平面EAC所成的锐角为30°?若存在,求出实数λ的值;若不存在,请说明理由. ,是否存在实数λ使得平面VCD与平面EAC所成的锐角为30°?若存在,求出实数λ的值;若不存在,请说明理由.
,是否存在实数λ使得平面VCD与平面EAC所成的锐角为30°?若存在,求出实数λ的值;若不存在,请说明理由.