题目内容
已知 ,
,
(1)对一切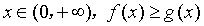 恒成立,求实数
恒成立,求实数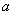 的取值范围;
的取值范围;
(2)当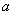 =1时,求函数
=1时,求函数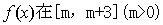 上的最小值和最大值;
上的最小值和最大值;
(3)证明:对一切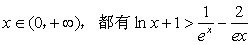 成立。
成立。
解:(1)对一切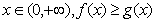 恒成立,即
恒成立,即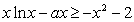 恒成立.也就是-
恒成立.也就是-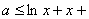
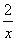 在
在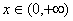 恒成立.
恒成立.
令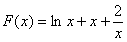 ,
,
则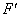
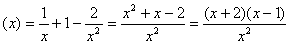 ,
,
在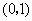 上
上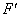
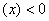 ,在
,在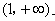 上
上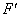
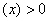 ,因此,
,因此,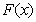 在
在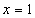 处取极小值,也是最小值,即
处取极小值,也是最小值,即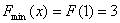 ,所以-
,所以-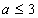
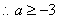 .
.
(2)当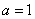 时,
时,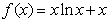 ,
,
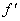
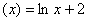 ,由
,由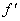
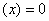 得
得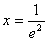 .
.
①当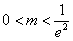 时,在
时,在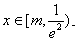 上
上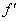
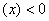 ,在
,在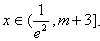 上
上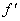
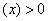
因此,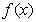 在
在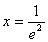 处取得极小值,也是最小值.
处取得极小值,也是最小值. 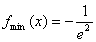 .
.
由于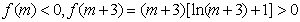
因此,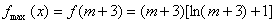
②当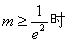 ,
,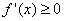 ,因此
,因此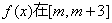 上单调递增,所以
上单调递增,所以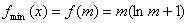 ,
, 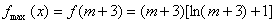
(3)证明:问题等价于证明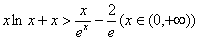 ,
,
由(Ⅱ)知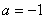 时,
时,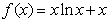 的最小值是
的最小值是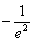 ,
,
当且仅当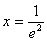 时取得,
时取得,
设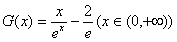 ,则
,则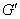
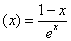 ,易知
,易知
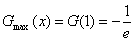 ,当且仅当
,当且仅当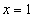 时取到,
时取到,
但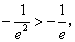 从而可知对一切
从而可知对一切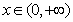 ,都有
,都有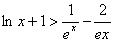 成立.
成立.

练习册系列答案
相关题目
在某种新型材料的研制中,实验人员获得了右边一组实验数据:现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是
( )
|
| 1.99 | 3 | 4 | 5.1 | 6.12 |
|
| 1.5 | 4.04 | 7.5 | 12 | 18.01 |
A. 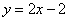 B.
B. 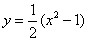
B.C.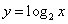 D.
D. 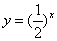
 是定义在R上且周期为2的函数,在区间
是定义在R上且周期为2的函数,在区间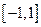 上,
上, 其中
其中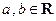 .若
.若 ,则
,则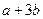 的值为 .
的值为 . :“若
:“若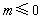 ,则
,则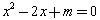 有实数解”的逆命题;命题
有实数解”的逆命题;命题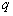 :“若函数
:“若函数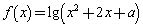 的值域为
的值域为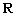 ,则
,则 ”.以下四个结论:
”.以下四个结论: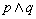 是假命题;③
是假命题;③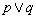 是假命题;④
是假命题;④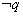 为假命题.
为假命题. ,则
,则 .
. 为纯虚数,求实数
为纯虚数,求实数 的值。
的值。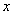
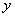
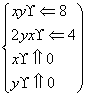 且z=5y-x的最大值为a,最小值为b,
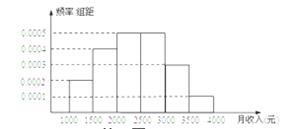
且z=5y-x的最大值为a,最小值为b,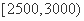 (元)月收入段应抽出
(元)月收入段应抽出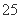 B.
B.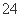 C.
C.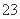 D.
D.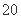
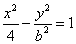 的右焦点与抛物线
的右焦点与抛物线 的焦点重合,则该双曲线的焦点到其渐近线的距离等于( )
的焦点重合,则该双曲线的焦点到其渐近线的距离等于( )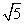 B.
B.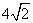 C.
C. D.
D.