题目内容
设正项数列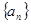 的前
的前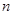 项和是
项和是 ,若
,若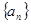 和{
和{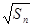 }都是等差数列,且公差相等,则
}都是等差数列,且公差相等,则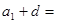
【答案】

【解析】
试题分析:设公差为d,首项a1,由于 和{
和{ }都是等差数列,且公差相等,,
}都是等差数列,且公差相等,, 两端平方得:4(2a1+d)=a1+3a1+3d+2
两端平方得:4(2a1+d)=a1+3a1+3d+2 ,两端再平方得:16a12+8a1d+d2=4a1(3a1+3d),∴4a12-4a1d+d2=0, d=2a1,又两数列公差相等a2-a1=d=2a1,解得
,两端再平方得:16a12+8a1d+d2=4a1(3a1+3d),∴4a12-4a1d+d2=0, d=2a1,又两数列公差相等a2-a1=d=2a1,解得 故可知
故可知

考点:等差数列
点评:本题考查等差数列的性质,考查等差中项的性质,考查化归与方程思想,属于难题.

练习册系列答案
相关题目
 的前
的前 项和
项和 ,且满足
,且满足 .
. 的值,猜想
的值,猜想 是数列
是数列 的前
的前 .
.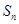 是正项数列
是正项数列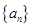 的前
的前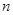 项和,且
项和,且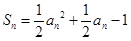 (
(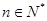 ).
).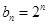 ,设
,设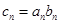 ,求数列
,求数列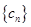 的前
的前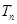 .
.