当k取何值时.方程组$\left\{\begin{array}{l}{y=kx+2}\\{{y}^{2}-4x-2y+1=0}\end{array}\right.$有两组不同的实数解．题目和参考答案——青夏教育精英家教网——

题目内容

10．当k取何值时，方程组$\left\{\begin{array}{l}{y=kx+2}\\{{y}^{2}-4x-2y+1=0}\end{array}\right.$有两组不同的实数解．

分析可化为函数y=kx+2与y²-4x-2y+1=0的图象有两个不同的交点，作图求解即可．

解答解：∵方程组$\left\{\begin{array}{l}{y=kx+2}\\{{y}^{2}-4x-2y+1=0}\end{array}\right.$有两组不同的实数解，
∴函数y=kx+2与y²-4x-2y+1=0的图象有两个不同的交点，
作函数y=kx+2与y²-4x-2y+1=0的图象如下，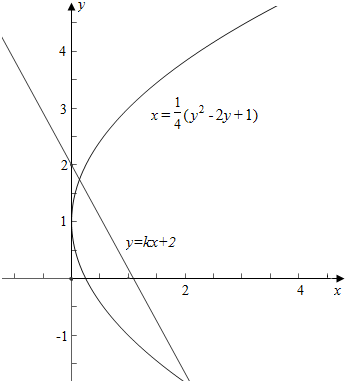

由图象可知，k＜0．

点评本题考查了方程的根与函数的图象的关系应用．

练习册系列答案

名师点拨课时作业甘肃教育出版社系列答案

小学奥数举一反三系列答案

新课标初中单元测试卷系列答案

口算应用一卡通系列答案

首席期末8套卷系列答案

新课标单元检测卷系列答案

同步训练全优达标测试卷系列答案

高考总复习三维设计系列答案

新课标小学毕业总复习系列答案

中考必备中考试卷精选系列答案

相关题目

20．已知$f（x）=cosx•cos（{x-\frac{π}{3}}）+a+\frac{1}{2}$．
（1）求f（x）的周期及递增区间；
（2）当$x∈[{0，\frac{π}{2}}]$时，f（x）的最小值为2，求a的值．

1．f（x）=x²-ax+b（a，b∈R），A={x|f（x）-x=0，x∈R}，B={x|f（x）-ax=0，x∈R}．若-3∈A，1∈A，用列举法表示集合B为{$-3+2\sqrt{3}$，$-3-2\sqrt{3}$}．

18．已知命题p：若x＞y，则-x＜-y；命题q：若x＜y，则x²＜y²．在命题：①p且q；②p或q；③p且非q；④非p或q中，真命题是②③．

5．过点M（-2，0）的直线l与抛物线y²=4x交于不同的两点A和B
（1）求直线l斜率的范围
（2）是否存在这样的直线l，使$\overrightarrow{MA}=\overrightarrow{AB}$，若存在，求出l的方程；反之，说明理由．

已知A是抛物线y²=4x上的一点，以点A和点B（2，0）为直径的圆C交直线x=1于M，N两点．直线l与AB平行，且直线l交抛物线于P，Q两点．
（Ⅰ）求线段MN的长；
（Ⅱ）若$\overrightarrow{OP}$$•\overrightarrow{OQ}$=-3，且直线PQ与圆C相交所得弦长与|MN|相等，求直线l的方程．

2．抛物线y=4x²上的一点M到焦点的距离为1，则点M的纵坐标是（　　）

$\frac{17}{16}$

$\frac{15}{16}$

19．在△ABC中，角A、B、C所对的边分别是a、b、c，若$\frac{a}{sinA}$=$\frac{b}{cosB}$=$\frac{c}{cosC}$则△ABC的形状是（　　）

	A．	等边三角形		B．	等腰直角三角形
	C．	直角非等腰三角形		D．	等腰非直角三角形

20．已知向量$\overrightarrow{a}$=（1，1），$\overrightarrow{b}$=（2，-3），当k为何值时，
（1）k$\overrightarrow{a}$-2$\overrightarrow{b}$与$\overrightarrow{a}$+$\overrightarrow{b}$垂直？
（2）k$\overrightarrow{a}$-2$\overrightarrow{b}$与$\overrightarrow{a}$+$\overrightarrow{b}$平行？平行时它们是同向还是反向？