题目内容
在△ABC中,若B=
,且a+c=
b,求角A的大小.
| π |
| 3 |
| 3 |
考点:余弦定理
专题:解三角形
分析:由题意和余弦定理化简可得ac=
b2,由正弦定理列出方程组求出sinA,由内角的范围和内角和定理求出角A.
| 2 |
| 3 |
解答:
解:由题意得,B=
,且a+c=
b,
由余弦定理得,b2=a2+c2-2accosB,
则b2=a2+c2-ac=(a+c)2-3ac,
由a+c=
b得,(a+c)2=3b2代入上式得,ac=
b2,
因为B=
,且a+c=
b,ac=
b2
所以由正弦定理得,
,即
,
解得sinA=1或
,
当sinA=1时,则A=
;当sinA=
时,则A=
或
;
当A=
时,A+B>π,则舍去,
综上可得,A=
或
.
| π |
| 3 |
| 3 |
由余弦定理得,b2=a2+c2-2accosB,
则b2=a2+c2-ac=(a+c)2-3ac,
由a+c=
| 3 |
| 2 |
| 3 |
因为B=
| π |
| 3 |
| 3 |
| 2 |
| 3 |
所以由正弦定理得,
|
|
解得sinA=1或
| 1 |
| 2 |
当sinA=1时,则A=
| π |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
当A=
| 5π |
| 6 |
综上可得,A=
| π |
| 2 |
| π |
| 6 |
点评:本题考查正弦、弦定理的灵活应用,三角形的内角和定理,以及内角的范围,容易忽略三角形中的角的范围和关系.

练习册系列答案
相关题目
下列结论能成立的是( )
A、sinα=
| ||||
B、tanα=2且
| ||||
C、tanα=1且cosα=
| ||||
D、sinα=1且tanα•cosα=
|
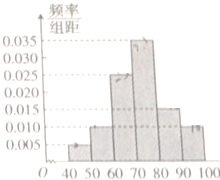 某市从2014届高中毕业生中抽取1000名学生的数学成绩作为样本进行统计,其频率分布直方图如图所示,则这1000名学生的数学平均成绩的最大值可能为( )
某市从2014届高中毕业生中抽取1000名学生的数学成绩作为样本进行统计,其频率分布直方图如图所示,则这1000名学生的数学平均成绩的最大值可能为( )| A、67.50 |
| B、72.50 |
| C、76.50 |
| D、77.50 |
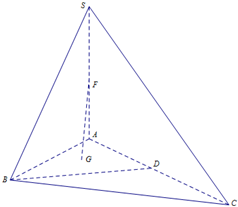 在三棱锥S-ABC中,SA⊥平面ABC,AB⊥AC.
在三棱锥S-ABC中,SA⊥平面ABC,AB⊥AC.