题目内容
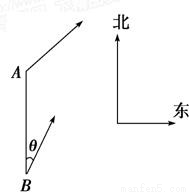
 如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15
如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15| 2 |
| 1 |
| 2 |
(Ⅰ)求4小时后甲船到B岛的距离为多少海里?
(Ⅱ)若两船能相遇,求m.
分析:(I)先求AC距离,再再三角形中利用余弦定理可求;(II)设两船在M处相遇,则关键是求出BM及相遇时的时间.
解答:解:(I)设4小时后甲船航行到C处,AC=60
,由余弦定理得BC=20
海里
(II)设两船在M处相遇,sinAMB=sin(450-θ)=
,由正弦定理
=
,∴AM=40
,从而有BM=40
,又时间t=
=
,∴m=
=15
| 2 |
| 34 |
(II)设两船在M处相遇,sinAMB=sin(450-θ)=
| ||
| 10 |
| AM |
| sinθ |
| AB |
| sin∠AMB |
| 2 |
| 5 |
40
| ||
15
|
| 8 |
| 3 |
40
| ||
|
| 5 |
点评:本题主要考查了解三角形问题的实际应用.考查了学生综合分析问题和解决的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15
如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15 如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15
如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15 的方向作匀速直线航行,速度为
的方向作匀速直线航行,速度为 海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东
海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东 的方向作匀速直线航行,速度为
的方向作匀速直线航行,速度为 海里/小时。
海里/小时。
 。
。 时,求两船出发后多长时间距离最近,最近距离为多少海里?
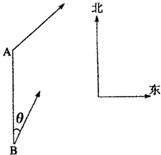
时,求两船出发后多长时间距离最近,最近距离为多少海里?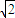 海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东θ(tanθ=
海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东θ(tanθ= )的方向作匀速直线航行,速度为10
)的方向作匀速直线航行,速度为10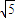 海里/小时.
海里/小时.