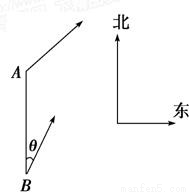
题目内容
 如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15
如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15| 2 |
| 1 |
| 2 |
(1)若两船能相遇,求m.
(2)当m=10
| 5 |
分析:(1)设两船在M处相遇,利用正弦定理,即可求出BM,然后求出相遇时的时间.
(2)以A为原点,BA所在直线为y轴,建立直角坐标系,设出在t时刻甲、乙两船分别在P(x1,y1)Q(x2,y2)处,
求出P、Q坐标|PQ|=
利用配方法求出最小值.
(2)以A为原点,BA所在直线为y轴,建立直角坐标系,设出在t时刻甲、乙两船分别在P(x1,y1)Q(x2,y2)处,
求出P、Q坐标|PQ|=
| (x2- x1)2+(y2- y1)2 |
解答:解:(1)因为tanθ=
,
,解得sinθ=
,cosθ=
;
甲船由A岛出发向北偏东45°的方向作匀速直线航行,
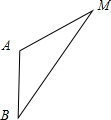
设两船在M处相遇,sin∠AMB=sin(45°-θ)=sin45°cosθ-cos45°sinθ=
,
由正弦定理
=
,
=
,
∴AM=40
,
从而有BM=40
,
又时间t=
=
=
,
∴m=
=
=15
.
(2)以A为原点,BA所在直线为y轴,建立直角坐标系,
设在t时刻甲、乙两船分别在P(x1,y1)Q(x2,y2)处,
则由tanθ=
,cosθ=
,sinθ=
,
,
,
|PQ|=
=
=
=
≥20
.
∴当且仅当t=4时|PQ|取得最小值20
.
即两船出发后4小时时间距离最近,最近距离为20
海里.
| 1 |
| 2 |
|
| ||
| 5 |
2
| ||
| 5 |
甲船由A岛出发向北偏东45°的方向作匀速直线航行,
设两船在M处相遇,sin∠AMB=sin(45°-θ)=sin45°cosθ-cos45°sinθ=
| ||
| 10 |

由正弦定理
| AM |
| sinθ |
| AB |
| sin∠AMB |
| AM | ||||
|
| 40 | ||||
|
∴AM=40
| 2 |
从而有BM=40
| 5 |
又时间t=
| AM | ||
15
|
40
| ||
15
|
| 8 |
| 3 |
∴m=
| BM |
| t |
40
| ||
|
| 5 |
(2)以A为原点,BA所在直线为y轴,建立直角坐标系,
设在t时刻甲、乙两船分别在P(x1,y1)Q(x2,y2)处,
则由tanθ=
| 1 |
| 2 |
2
| ||
| 5 |
| ||
| 5 |
|
|

|PQ|=
| (x2- x1)2+(y2- y1)2 |
=
| (10t- 15t )2+(20t-40-15t)2 |
=
| 50t2-400t+1600 |
=
| 50(t-4)2+800 |
| 2 |
∴当且仅当t=4时|PQ|取得最小值20
| 2 |
即两船出发后4小时时间距离最近,最近距离为20
| 2 |
点评:本题主要考查了解三角形问题的实际应用.考查余弦定理以及配方法的应用,考查了学生综合分析问题和解决的能力.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
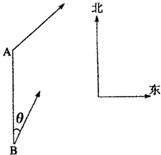 如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15
如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15 如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15
如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15 的方向作匀速直线航行,速度为
的方向作匀速直线航行,速度为 海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东
海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东 的方向作匀速直线航行,速度为
的方向作匀速直线航行,速度为 海里/小时。
海里/小时。
 。
。 时,求两船出发后多长时间距离最近,最近距离为多少海里?
时,求两船出发后多长时间距离最近,最近距离为多少海里?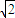 海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东θ(tanθ=
海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东θ(tanθ= )的方向作匀速直线航行,速度为10
)的方向作匀速直线航行,速度为10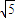 海里/小时.
海里/小时.