题目内容
13.已知可行域$\left\{\begin{array}{l}{y≥0}\\{x-y+\sqrt{2}≥0}\\{x+y-\sqrt{2}≤0}\end{array}\right.$的外接圆C与x轴交于A1、A2点,M(1,0).(1)求圆C的方程;
(2)设P点是圆C上异于A1、A2的动点,过O作直线PM的垂线交L:x=2于Q点,判断直线PQ与圆C的位置关系并证明.
分析 (1)由题意可知,可行域是以A1、A2,M为顶点的三角形.因为kA1M•kA2M=-1,所以A1M⊥A2M,所以△A1A2M为直角三角形,外接圆C1的方程为x2+y2=2.
(2)设P(x0,y0)( ),则y02=2-x02,当x0=1时,OP⊥PQ,直线PQ与圆C1相切.当x0≠1时,kPF=,kOQ=-.当x0=0时,OP⊥PQ.当x0≠0时,kOP=,OP⊥PQ.综上,当x0≠±时,故直线PQ始终与圆C1相切
解答 解:(1)由题意可知,易得可行域如,是以A1(-$\sqrt{2}$,0),A2($\sqrt{2}$,0)及点B($\sqrt{2}$,0)为顶点的三角形(1分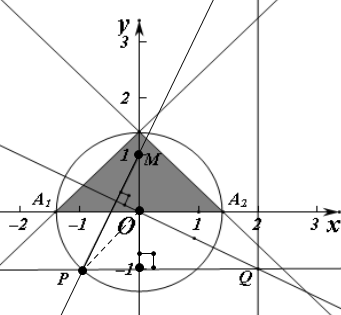
因为k${\;}_{{A}_{1}B}$•k${\;}_{{A}_{2}B}$=-1,所以A1B⊥A2B,
∴△A1A2B为直角三角形
∴外接圆C1是以原点O为圆心,线段|A1A2|=2$\sqrt{2}$为直径的圆,
故其方程为x2+y2=2(3分)
(2)设P($\sqrt{2}$cosθ,$\sqrt{2}$sinθ),Q(2,y),所以$\overrightarrow{PM}$=(1-$\sqrt{2}$cosθ,-$\sqrt{2}$sinθ),则$\overrightarrow{PM}•\overrightarrow{OQ}$=0,则2$\sqrt{2}$cosθ-2+$\sqrt{2}$ysinθ=0,
则$\overrightarrow{PO}•\overrightarrow{PQ}$=(-$\sqrt{2}$cos$θ,-\sqrt{2}$sinθ)•(2-$\sqrt{2}$cosθ,y-$\sqrt{2}$sinθ)=-2$\sqrt{2}$cosθ+2cos2θ-$\sqrt{2}$ysinθ+2sin2θ=2-2$\sqrt{2}$cosθ-$\sqrt{2}$ysinθ=0,
所以$\overrightarrow{PO}⊥\overrightarrow{PQ}$,
故PQ与圆相切.
点评 本题考查了平面区域、曲线方程以及直线与圆位置关系的判断;利用向量的数量积为0,判断直线垂直是常用的方法.

| A. | an=2n-1 | B. | an=2n+1 | C. | an=$\left\{{\begin{array}{l}{2(n=1)}\\{2n-1(n>1)}\end{array}}\right.$ | D. | an=$\left\{{\begin{array}{l}{2(n=1)}\\{2n+1(n>1)}\end{array}}\right.$ |
| A. | $\frac{1}{a}$>$\frac{1}{b}$ | B. | $\frac{b}{a}$>1 | C. | a2<b2 | D. | ab<a+b |
| A. | (-∞,-$\frac{2}{3}$] | B. | (-∞,$\frac{1}{3}$] | C. | [$\frac{1}{3}$,+∞) | D. | [-$\frac{1}{3}$,+∞] |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |