题目内容
若函数f（x）=sinωx+cosωx（ω≠0）对任意实数x都有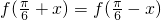
，则
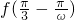的值等于
- A.-1
- B.1
- C.
- D.
A
分析：利用两角和的正弦公式化简函数的解析式为sin（ωx+
），根据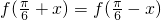，可得函数的图象关于直线x=
对称，故有ω•+=kπ+
，k∈z．解得ω的值，代入 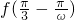的解析式化简求得结果．
解答：∵函数f（x）=sinωx+cosωx（ω≠0）=sin（ωx+），
对任意实数x都有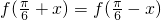，故函数的图象关于直线x=对称，
故有ω•+=kπ+，k∈z，∴ω=6k+
．
令ω=，则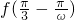=sin[ω•（
）+]=sin（-）=-1，
故选A．
点评：本题主要考查两角和的正弦公式，正弦函数的对称性，属于中档题．
分析：利用两角和的正弦公式化简函数的解析式为
sin（ωx+），根据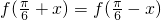，可得函数的图象关于直线x=对称，故有ω•+=kπ+，k∈z．解得ω的值，代入 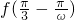的解析式化简求得结果．解答：∵函数f（x）=sinωx+cosωx（ω≠0）=
sin（ωx+），对任意实数x都有
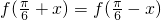，故函数的图象关于直线x=对称，故有ω•
+=kπ+，k∈z，∴ω=6k+．令ω=
，则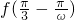=sin[ω•（）+]=sin（-）=-1，故选A．
点评：本题主要考查两角和的正弦公式，正弦函数的对称性，属于中档题．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
若函数f（x）同时满足下列三个性质：
①最小正周期为π；
②图象关于直线x=
对称；
③在区间[-
，
]上是增函数．
则y=f（x）的解析式可以是（ ）
①最小正周期为π；
②图象关于直线x=
| π |
| 3 |
③在区间[-
| π |
| 6 |
| π |
| 3 |
则y=f（x）的解析式可以是（ ）
A、y=sin（2x-
| ||||
B、y=sin（
| ||||
C、y=cos（2x-
| ||||
D、y=cos（2x+
|
若函数f（x）=
cos（3x-θ）-sin（3x-θ）为奇函数，则θ等于（ ）
| 3 |
| A、kπ（k∈Z） | ||
B、kπ+
| ||
C、kπ+
| ||
D、kπ-
|