题目内容
如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=![]() (x>0)图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为( )
(x>0)图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为( )
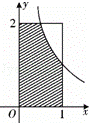
|
| A. |
| B. |
| C. |
| D. |
|
考点:
定积分;几何概型.
专题:
计算题.
分析:
先由积分的知识求解阴影部分的面积,然后可求试验的区域所对应的矩形的面积,由几何概率的求解公式代入可求
解答:
解:本题是几何概型问题,
区域E的面积为:S=2×![]() =1+
=1+![]() =1﹣ln
=1﹣ln![]() =1+ln2
=1+ln2
∴“该点在E中的概率”事件对应的区域面积为 1+ln2,
矩形的面积为2
由集合概率的求解可得P=![]()
故选C
点评:
本题综合考查了反比例函数的图象,几何概型,及定积分在求面积中的应用,考查计算能力与转化思想.属于基础题.

练习册系列答案
相关题目
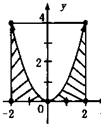 如图,设D是图中边长为4的正方形区域,E是D内函数y=x2图象下方的点构成的区域.在D内随机取一点,则该点在E中的概率为( )
如图,设D是图中边长为4的正方形区域,E是D内函数y=x2图象下方的点构成的区域.在D内随机取一点,则该点在E中的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,设D是图中边长分别为2和4的矩形区域,E是D内位于函数y=x2图象下方的区域(阴影部分),向D内随机抛掷30个点,则落在E内的点的个数约为( )
如图,设D是图中边长分别为2和4的矩形区域,E是D内位于函数y=x2图象下方的区域(阴影部分),向D内随机抛掷30个点,则落在E内的点的个数约为( )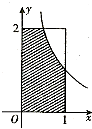 如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数
如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数 (2012•道里区三模)如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=
(2012•道里区三模)如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=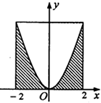 如图,设D是图中边长为4的正方形区域,E是D内函数y=x2图象下方的点构成的区域.向D中随机投一点,则该点落入E中的概率为
如图,设D是图中边长为4的正方形区域,E是D内函数y=x2图象下方的点构成的区域.向D中随机投一点,则该点落入E中的概率为